Feller process
2020 Mathematics Subject Classification: Primary: 60J35 [MSN][ZBL]
A homogeneous Markov process  ,
,  , where
, where  is an additive sub-semi-group of the real axis
is an additive sub-semi-group of the real axis  , with values in a topological space
, with values in a topological space 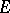 with a topology
with a topology  and a Borel
and a Borel  -algebra
-algebra  , the transition function
, the transition function  ,
, 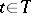 ,
, 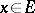 ,
,  , of which has a certain property of smoothness, namely that for a continuous bounded function
, of which has a certain property of smoothness, namely that for a continuous bounded function  the function
the function
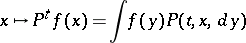 |
is continuous. This requirement on the transition function is natural because the transition operators 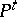 ,
,  , acting on the space of bounded Borel functions, leave invariant the space
, acting on the space of bounded Borel functions, leave invariant the space 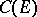 of continuous bounded functions, that is, the semi-group
of continuous bounded functions, that is, the semi-group  of transition operators can be considered as acting on
of transition operators can be considered as acting on 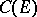 . The first semi-groups of this type were studied by W. Feller (1952, see [1]).
. The first semi-groups of this type were studied by W. Feller (1952, see [1]).
As a rule, one imposes additional conditions on the topological space; usually  is a locally compact metrizable space. In this case, a Feller process that satisfies the condition of stochastic continuity admits a modification that is a standard Markov process (see Markov process, the strong Markov property). Conversely, a standard Markov process is a Feller process for a natural topology
is a locally compact metrizable space. In this case, a Feller process that satisfies the condition of stochastic continuity admits a modification that is a standard Markov process (see Markov process, the strong Markov property). Conversely, a standard Markov process is a Feller process for a natural topology 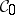 ; a basis of
; a basis of 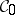 is constituted by the sets
is constituted by the sets 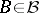 such that the first exit moment
such that the first exit moment  from
from 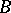 almost-surely satisfies
almost-surely satisfies 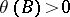 if the process starts in
if the process starts in 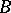 (see [1]).
(see [1]).
An important subclass of Feller processes is formed by the strong Feller processes [2]; in this case a stricter smoothness condition is imposed on the transition function: The function 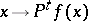 must be continuous for every bounded Borel function
must be continuous for every bounded Borel function  . If, moreover, the function
. If, moreover, the function 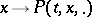 is continuous in the variation norm in the space of bounded measures, then the Markov process corresponding to this transition function is called a strong Feller process in the narrow sense. If the transition functions
is continuous in the variation norm in the space of bounded measures, then the Markov process corresponding to this transition function is called a strong Feller process in the narrow sense. If the transition functions 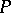 and
and 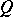 correspond to strong Feller processes, then their composition
correspond to strong Feller processes, then their composition 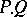 corresponds to a strong Feller process in the narrow sense under the usual assumptions on
corresponds to a strong Feller process in the narrow sense under the usual assumptions on 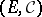 . Non-degenerate diffusion processes (cf. Diffusion process) are strong Feller processes (see [3]). A natural generalization of strong Feller processes are Markov processes with a continuous component (see [4]).
. Non-degenerate diffusion processes (cf. Diffusion process) are strong Feller processes (see [3]). A natural generalization of strong Feller processes are Markov processes with a continuous component (see [4]).
If 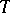 is a subset of the natural numbers, then a Feller process
is a subset of the natural numbers, then a Feller process 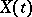 ,
, 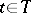 , is called a Feller chain. An example of a Feller chain is provided by a random walk on the line
, is called a Feller chain. An example of a Feller chain is provided by a random walk on the line 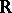 : a sequence
: a sequence  ,
, 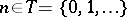 , where
, where 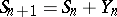 , and
, and 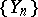 is a sequence of independent identically-distributed random variables. Here the random walk
is a sequence of independent identically-distributed random variables. Here the random walk 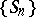 is a strong Feller chain if and only if the distribution of
is a strong Feller chain if and only if the distribution of 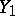 has a density.
has a density.
There is a natural generalization for Feller processes of the classification of the states of a Markov chain with a countable number of states (see Markov chain). Two states  and
and  in
in  are in communication if for any neighbourhoods
are in communication if for any neighbourhoods 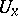 of
of  and
and 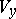 of
of 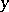 there are
there are 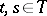 such that
such that 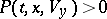 and
and  (chains with a countable set of states are Feller chains with the discrete topology). Ergodic properties and methods for investigating them have a definite character for Feller processes in comparison to classical ergodic theory. The "most-regular" behaviour is found with irreducible (topologically-indecomposable) Feller processes; these are Feller processes all states of which are in communication (see [7]). Here the ergodic properties of a Feller process are of a comparatively weak nature.
(chains with a countable set of states are Feller chains with the discrete topology). Ergodic properties and methods for investigating them have a definite character for Feller processes in comparison to classical ergodic theory. The "most-regular" behaviour is found with irreducible (topologically-indecomposable) Feller processes; these are Feller processes all states of which are in communication (see [7]). Here the ergodic properties of a Feller process are of a comparatively weak nature.
As an example one can compare properties such as recurrence for a Markov chain with a general space of states. Suppose that for any initial state 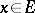 and any set
and any set  in
in 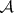 it is almost-surely true that
it is almost-surely true that 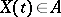 for an infinite set of values of the time
for an infinite set of values of the time 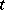 (
(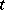 takes values in the natural numbers). If
takes values in the natural numbers). If  is a system of sets of the form
is a system of sets of the form 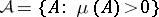 , where
, where 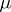 is some measure, then one obtains the recurrence property of a chain in the sense of Harris (see [8]), and if for the Feller process one chooses as
is some measure, then one obtains the recurrence property of a chain in the sense of Harris (see [8]), and if for the Feller process one chooses as  the topology
the topology  on
on 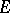 , the diffusion (topological recurrence) property is obtained (see [7]). A random walk
, the diffusion (topological recurrence) property is obtained (see [7]). A random walk 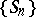 for which
for which 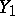 has finite expectation
has finite expectation 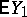 is a diffusion Feller chain if and only if
is a diffusion Feller chain if and only if 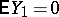 , and if the distribution of
, and if the distribution of  is not arithmetic, then
is not arithmetic, then 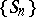 is moreover recurrent in the sense of Harris only if for some
is moreover recurrent in the sense of Harris only if for some  the distribution of
the distribution of 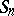 has an absolutely-continuous component.
has an absolutely-continuous component.
From the formal point of view, the theory of Markov chains with a general state space 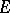 can be reduced to the study of Feller chains with a compact state space
can be reduced to the study of Feller chains with a compact state space  — the extension of
— the extension of 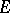 obtained by means of the Gel'fand–Naimark theorem (see Banach algebra and [9]). This extension, however, is "too large" ; other constructions of Feller extensions are also possible for Markov chains (see [10]).
obtained by means of the Gel'fand–Naimark theorem (see Banach algebra and [9]). This extension, however, is "too large" ; other constructions of Feller extensions are also possible for Markov chains (see [10]).
The theory of Feller processes and Feller chains is also a probabilistic generalization of topological dynamics, since a deterministic (degenerate) Feller process  ,
,  , corresponds to the dynamical system
, corresponds to the dynamical system  , where the mapping
, where the mapping 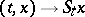 from
from  into
into 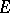 is continuous and
is continuous and 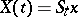 (almost-surely).
(almost-surely).
References
| [1] | E.B. Dynkin, "Markov processes" , 1–2 , Springer (1965) (Translated from Russian) |
| [2] | I.V. Girsanov, "On transforming a certain class of stochastic processes by absolutely continuous substitution of measures" Theor. Probab. Appl. , 5 : 3 (1960) pp. 285–301 Teor. Veroyatnost. i Primenen. , 5 : 3 (1960) pp. 314–330 |
| [3] | S.A. Molchanov, "Strong Feller property of diffusion processes on smooth manifolds" Theor. Probab. Appl. , 13 : 3 (1968) pp. 471–475 Teor. Veroyatnost. i Primenen. , 13 : 3 (1968) pp. 493–498 |
| [4] | P. Tuominen, R. Tweedie, "Markov chains with continuous components" Proc. London Math. Soc. , 38 (1979) pp. 89–114 |
| [5] | S. Foguel, "The ergodic theory of positive operators on continuous functions" Ann. Scuola Norm. Sup. Pisa , 27 : 1 (1973) pp. 19–51 |
| [6] | R. Sine, "Sample path convergence of stable Markov processes II" Indiana Univ. Math. J. , 25 : 1 (1976) pp. 23–43 |
| [7] | S.N. Smirnov, "On the asymptotic behavior of Feller chains" Soviet Math. Dokl. , 25 : 2 (1982) pp. 399–403 Dokl. Akad. Nauk SSSR , 263 : 3 (1982) pp. 554–558 |
| [8] | D. Revuz, "Markov chains" , North-Holland (1975) |
| [9] | A.I. Zhdanok, "Ergodic theorems for nonsmooth Markov processes" , Topological spaces and their mappings , Riga (1981) pp. 18–33 (In Russian) (English summary) |
| [10] | M.G. Shur, "Invariant measures for Markov chains and Feller extensions of chains" Theory Probab. Appl. , 26 : 3 (1981) pp. 485–497 Teor. Veroyatnost. i Primenen. , 26 : 3 (1981) pp. 496–509 |
Comments
In the West a Feller process is usually indexed by 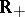 (and not by
(and not by 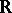 ). Feller processes are important for three main reasons:
). Feller processes are important for three main reasons:
a) numerous natural (homogeneous) Markov processes are Feller; e.g., a diffusion process, a stochastic process with stationary increments, among them a Wiener process and a Poisson process;
b) the notion of a Feller semi-group (i.e. a transition-operator semi-group 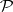 as defined in the main article) lies at the interface between the stochastic and the analytic study of semi-groups of linear operators (see also Semi-group of operators);
as defined in the main article) lies at the interface between the stochastic and the analytic study of semi-groups of linear operators (see also Semi-group of operators);
c) by way of the so-called Ray–Knight compactification it is possible to look at a strong Markov process as if it were "almost" a Feller process (with a nice topology on the state space), and so the make use of the smoothness of the latter.
References
| [a1] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , C , North-Holland (1988) (Translated from French) |
| [a2] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1966) pp. Chapt. X |
| [a3] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) pp. Chapt. XIV |
| [a4] | K.L. Chung, "Lectures from Markov processes to Brownian motion" , Springer (1982) |
| [a5] | A.D. [A.D. Ventsel'] Wentzell, "A course in the theory of stochastic processes" , McGraw-Hill (1981) (Translated from Russian) |
| [a6] | T.G. Kurtz, "Markov processes" , Wiley (1986) |
Feller process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Feller_process&oldid=23608