Köthe-Toeplitz dual

For any subset 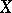of the set 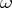of all sequences 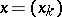, the set

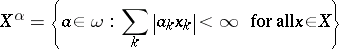is called a Köthe–Toeplitz or 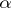-dual of 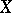. These duals play an important role in the representation of linear functionals (cf. Linear functional) and the characterization of matrix transformations between sequence spaces. They are special cases of the more general multiplier sequence spaces

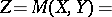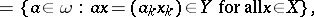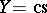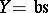which for and , the sets of convergent or bounded series, reduce to 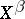and 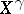, the so-calle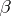d - and 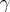-duals, also referred to as Köthe–Toeplitz duals by some authors (see [a2]). If denotes any of the symbols 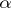, 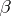or 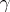, then for all 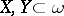one has: 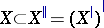, , 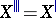and 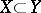implies 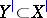. A set 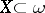is called (-) perfect if ; 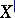is perfect, so is 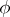(the set of sequences that terminate in naughts); the set of convergent sequences is not perfect. For any 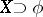, 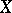and 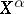(and analogously 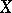and 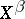) are in duality with respect to the bilinear functional 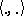on 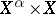defined by 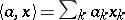, and various topologies may be introduced on 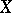and 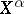, usually on 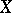the weak 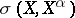, the Mackey 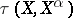, or the normal topology is taken (see [a1]; cf. also Weak topology; Mackey topology; Normal space). If 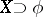and 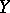are BK-spaces (i.e., Banach FK-spaces; cf. FK-space), then 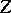is a BK-space with respect to 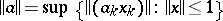. However, if 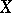is not a BK space, then 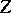need not even be an FK-space; for instance, 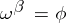is not an FK-space. The 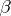-dual of an FK space 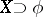is contained in its continuous dual 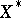in the following sense: The mapping 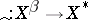defined by 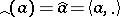(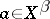) is linear and one-to-one; if 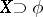has the AK-property (i.e. 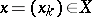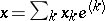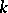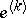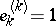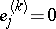every sequence has a unique representation , where for each , is the sequence with and if 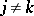), then is an isomorphism.

References

[a1]	W.H. Ruckle, "Sequence spaces" , Pitman (1989)
[a2]	A. Wilansky, "Summability through functional analysis" , North-Holland (1984)