Weyl-Otsuki space
Otsuki–Weyl space
An Otsuki space [a6], [a7] is a manifold 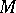 endowed with two different linear connections
endowed with two different linear connections 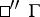 and
and 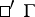 (cf. also Connections on a manifold) and a non-degenerate
(cf. also Connections on a manifold) and a non-degenerate 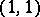 tensor field
tensor field 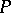 of constant rank (cf. also tensor analysis), where the connection coefficients
of constant rank (cf. also tensor analysis), where the connection coefficients 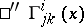 ,
, 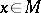 , are used in the computation of the contravariant, and the
, are used in the computation of the contravariant, and the 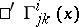 in the computation of the covariant, components of the invariant (covariant) differential of a tensor (vector). For a tensor field
in the computation of the covariant, components of the invariant (covariant) differential of a tensor (vector). For a tensor field 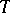 of type
of type 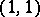 , the invariant differential
, the invariant differential 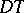 and the covariant differential
and the covariant differential 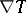 have the following forms
have the following forms
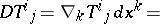 |
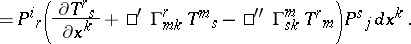 |
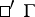 and
and 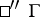 are connected by the relation
are connected by the relation
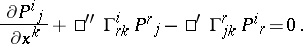 |
Thus, 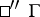 and
and 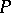 determine
determine 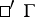 . T. Otsuki calls these a general connection. For
. T. Otsuki calls these a general connection. For 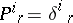 one obtains
one obtains 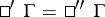 and the usual invariant differential.
and the usual invariant differential.
If 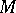 is endowed also with a Riemannian metric
is endowed also with a Riemannian metric 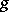 , then
, then  may be the Christoffel symbol
may be the Christoffel symbol 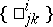 .
.
In a Weyl space 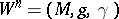 one has
one has 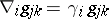 . A Weyl–Otsuki space
. A Weyl–Otsuki space 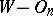 [a1] is a
[a1] is a 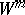 endowed with an Otsuki connection. The
endowed with an Otsuki connection. The 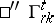 are defined here as
are defined here as
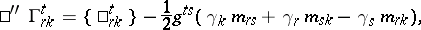 |
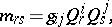 |
where 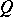 is the inverse of
is the inverse of 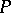 .
. 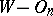 spaces were studied mainly by A. Moór [a2], [a3].
spaces were studied mainly by A. Moór [a2], [a3].
He extended the Otsuki connection also to affine and metrical line-element spaces, obtaining Finsler–Otsuki spaces 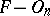 [a4], [a5] with invariant differential
[a4], [a5] with invariant differential
 |
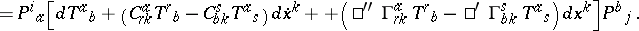 |
Here, all objects depend on the line-element 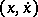 , the
, the 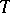 ,
, 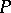 ,
, 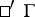 ,
, 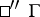 are homogeneous of order
are homogeneous of order  , and
, and 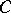 is a tensor.
is a tensor.
References
| [a1] | A. Moór, "Otsukische Übertragung mit rekurrenter Maß tensor" Acta Sci. Math. , 40 (1978) pp. 129–142 |
| [a2] | A. Moór, "Über verschiedene geodätische Abweichungen in Weyl–Otsukischen Räumen" Publ. Math. Debrecen , 28 (1981) pp. 247–258 |
| [a3] | A. Moór, "Über Transformationsgruppen in Weyl–Otsukischen Räumen" Publ. Math. Debrecen , 29 (1982) pp. 241–250 |
| [a4] | A. Moór, "Über die Begründung von Finsler–Otschukischen Räumen und ihre Dualität" Tensor N.S. , 37 (1982) pp. 121–129 |
| [a5] | A. Moór, "Über spezielle Finsler–Otsukische Räume" Publ. Math. Debrecen , 31 (1984) pp. 185–196 |
| [a6] | T. Otsuki, "On general connections. I" Math. J. Okayama Univ. , 9 (1959-60) pp. 99–164 |
| [a7] | T. Otsuki, "On metric general connections" Proc. Japan Acad. , 37 (1961) pp. 183–188 |
Weyl-Otsuki space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl-Otsuki_space&oldid=23137