Lévy inequality

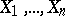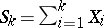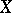An inequality for the distribution of the maximum of sums of independent random variables, centred around the corresponding medians. Let be independent random variables, let and let be the median (cf. Median (in statistics)) of the random variable ; then for any one has the Lévy inequalities

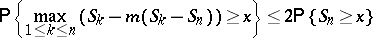and

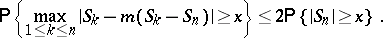Immediate consequences of these inequalities are the Lévy inequalities for symmetrically-distributed random variables :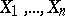

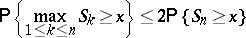and

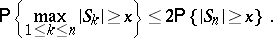The Lévy inequalities can be regarded as generalizations of the Kolmogorov inequality. The Lévy inequalities were obtained by P. Lévy [1] in the investigation of general problems on the convergence of distributions of sums of independent random variables to stable laws. There is also a generalization of them to martingales [2].

References

[1]	P. Lévy, "Théorie de l'addition des variables aléatoires" , Gauthier-Villars (1937)
[2]	M. Loève, "Probability theory" , Princeton Univ. Press (1963)