Cauchy-Riemann conditions

d'Alembert–Euler conditions

Conditions that must be satisfied by the real part 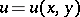and the imaginary part 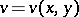of a complex function 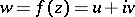, , for it to be monogenic and analytic as a function of a complex variable.

A function 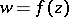, defined in some domain 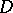in the complex -plane, is monogenic at a point , i.e. has a derivative at as a function of the complex variable , if and only if its real and imaginary parts and are differentiable at as functions of the real variables and 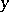, and if, moreover, the Cauchy–Riemann equations hold at that point:

(1)

If the Cauchy–Riemann equations are satisfied, then the derivative can be expressed in any of the following forms:

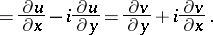A function , defined and single-valued in a domain , is analytic in if and only if its real and imaginary parts are differentiable functions satisfying the Cauchy–Riemann equations throughout . Each of the two functions and of class satisfying the Cauchy–Riemann equations (1) is a harmonic function of and ; the conditions (1) constitute conjugacy conditions of these two harmonic functions: Knowing one of them, the other may be found by integration.

The conditions (1) are valid for any two orthogonal directions and , with the same mutual orientations as the - and -axes, in the form:

For example, in polar coordinates , for :

Defining the complex differential operators by

one can rewrite the Cauchy–Riemann equations (1) as

Thus, a differentiable function of the variables and is an analytic function of if and only if .

For analytic functions of several complex variables , , 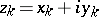, the Cauchy–Riemann equations constitute a system of partial differential equations (overdetermined when ) for the functions

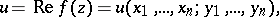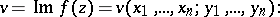(2)

or, in terms of the complex differentiation operators:

Each of the two functions and of class satisfying the conditions (2) is a pluriharmonic function of the variables and (). When the pluriharmonic functions constitute a proper subclass of the class of harmonic functions. The conditions (2) are conjugacy conditions for two pluriharmonic functions and : Knowing one of them, one can determine the other by integration.

The conditions (1) apparently occurred for the first time in the works of J. d'Alembert [1]. Their first appearance as a criterion for analyticity was in a paper of L. Euler, delivered at the Petersburg Academy of Sciences in 1777 [2]. A.L. Cauchy utilized the conditions (1) to construct the theory of functions, beginning with a memoir presented to the Paris Academy in 1814 (see [3]). The celebrated dissertation of B. Riemann on the fundamentals of function theory dates from 1851 (see [4]).

References

[1]	J. d'Alembert, "Essai d'une nouvelle théorie de la résistance des fluides" , Paris (1752)
[2]	L. Euler, Nova Acta Acad. Sci. Petrop. , 10 (1797) pp. 3–19
[3]	A.L. Cauchy, "Mémoire sur les intégrales définies" , Oeuvres complètes Ser. 1 , 1 , Paris (1882) pp. 319–506
[4]	"Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen komplexen Grösse" H. Weber (ed.) , Riemann's gesammelte math. Werke , Dover, reprint (1953) pp. 3–48 (Dover, reprint, 1953)
[5]	A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) pp. Chapt. 1 (Translated from Russian)
[6]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) pp. 1, Chapt. 1; 2, Chapt. 1 (In Russian)

References

[a1]	L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. 24–26