Buekenhout-Metz unital
A type of unital constructed from 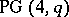 via the construction of a translation plane (cf. Translation surface). Let
via the construction of a translation plane (cf. Translation surface). Let 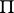 be a hyperplane of
be a hyperplane of  and let
and let 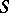 be a spread, that is a set of lines, necessarily
be a spread, that is a set of lines, necessarily 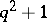 in number, partitioning
in number, partitioning 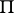 . Define an incidence structure
. Define an incidence structure  (cf. Incidence system), where the elements of
(cf. Incidence system), where the elements of 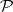 are the
are the 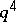 points of
points of 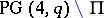 and the
and the 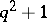 lines of
lines of 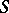 . The elements of
. The elements of 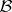 are the
are the  planes of
planes of 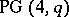 meeting
meeting 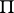 in precisely a line of
in precisely a line of 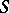 and the single element
and the single element 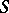 . Incidence is inclusion. Then
. Incidence is inclusion. Then 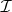 is a projective plane, which is Desarguesian (cf. Desargues geometry) if
is a projective plane, which is Desarguesian (cf. Desargues geometry) if 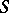 is regular, that is, if it has the property that three tranversals of three lines of
is regular, that is, if it has the property that three tranversals of three lines of 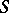 are transversals of
are transversals of  lines of
lines of 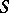 .
.
Now, let 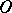 be an ovoid, that is, a set of
be an ovoid, that is, a set of  points, no three collinear, in a hyperplane
points, no three collinear, in a hyperplane 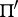 other than
other than 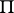 such that
such that 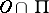 is the single point
is the single point 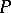 , where
, where 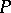 is not on the line
is not on the line 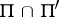 . Let
. Let 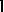 be the line of
be the line of  through
through 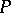 and let
and let 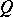 be a point of
be a point of 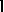 other than
other than 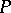 . Then, with
. Then, with 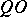 the cone with vertex
the cone with vertex 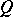 and base
and base 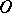 ,
,
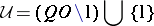 |
is the eponymous unital in  . If
. If 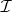 is Desarguesian, both the Tits ovoid when
is Desarguesian, both the Tits ovoid when 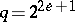 with
with 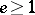 and a suitably chosen elliptic quadric for arbitrary
and a suitably chosen elliptic quadric for arbitrary 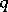 with
with 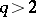 give a unital, also called in this case a Hermitian arc, that is not a Hermitian curve [a1], [a3]. An explicit equation of degree
give a unital, also called in this case a Hermitian arc, that is not a Hermitian curve [a1], [a3]. An explicit equation of degree 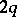 can be given [a2].
can be given [a2].
References
| [a1] | F. Buekenhout, "Existence of unitals in finite translation planes of order 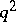 with a kernel of order with a kernel of order 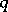 " Geom. Dedicata , 5 (1976) pp. 189–194 " Geom. Dedicata , 5 (1976) pp. 189–194 |
| [a2] | J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Oxford Univ. Press (1985) |
| [a3] | R. Metz, "On a class of unitals" Geom. Dedicata , 8 (1979) pp. 125–126 |
Buekenhout-Metz unital. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buekenhout-Metz_unital&oldid=22215