Bohman-Korovkin theorem
The starting point is the following theorem of P.P. Korovkin (1953) [a6], [a7]: for a given sequence 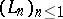 of positive linear operators on the space
of positive linear operators on the space 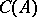 into itself (where
into itself (where 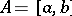 is a compact interval and
is a compact interval and 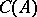 denotes the Banach space of all continuous real-valued functions on
denotes the Banach space of all continuous real-valued functions on 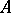 with the supremum norm
with the supremum norm 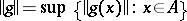 ), the relations
), the relations
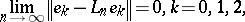 |
imply convergence:
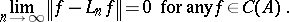 |
Here, the functions 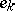 are defined by
are defined by 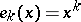 and
and 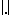 is the supremum norm on the interval
is the supremum norm on the interval 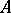 . An element
. An element 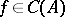 is positive (denoted by
is positive (denoted by 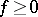 ) if
) if 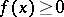 for all
for all 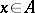 , and the linear operator
, and the linear operator 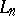 is positive if
is positive if 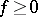 implies
implies 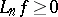 . One year earlier, in 1952, H. Bohman [a2] had proved this theorem for positive operators
. One year earlier, in 1952, H. Bohman [a2] had proved this theorem for positive operators 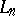 having a representation
having a representation
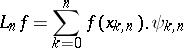 |
with 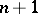 knots
knots 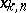 in the open interval
in the open interval 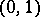 , and
, and 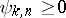 on
on 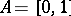 .
.
One says that the functions 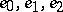 are a Korovkin set for (positive linear operators on)
are a Korovkin set for (positive linear operators on) 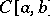 . Korovkin proved that a set of three functions in
. Korovkin proved that a set of three functions in 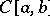 that replaces the set
that replaces the set 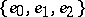 must be a Chebyshev system; he also proved that there are no sets of only two functions such that convergence for these two functions implies convergence for all
must be a Chebyshev system; he also proved that there are no sets of only two functions such that convergence for these two functions implies convergence for all 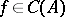 (cf. also Korovkin theorems; Korovkin-type approximation theory).
(cf. also Korovkin theorems; Korovkin-type approximation theory).
The results have been generalized to other compact Hausdorff spaces 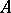 . For example, on the circle
. For example, on the circle 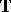 , the set of functions
, the set of functions 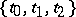 with
with 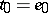 ,
, 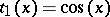 ,
, 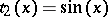 is a Korovkin set for
is a Korovkin set for 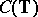 . As usual, one identifies the functions in
. As usual, one identifies the functions in 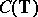 with the continuous
with the continuous 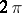 -periodic functions on
-periodic functions on 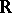 (cf, [a1], [a4]). On the
(cf, [a1], [a4]). On the 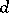 -dimensional cube
-dimensional cube 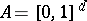 , the set of
, the set of 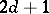 functions
functions 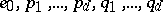 (with
(with 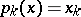 and
and 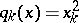 for
for 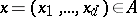 and
and 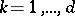 ) is a Korovkin set for
) is a Korovkin set for 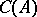 , but not a minimal Korovkin set.
, but not a minimal Korovkin set.
There is also the following generalization. Let 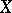 be a Banach lattice, let
be a Banach lattice, let 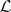 be the class of all positive linear operators on
be the class of all positive linear operators on 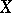 , and let
, and let 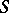 be a fixed subset of
be a fixed subset of 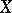 . Then the Korovkin closure (or shadow, or Korovkin hull)
. Then the Korovkin closure (or shadow, or Korovkin hull) 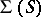 of
of 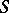 is the set of all
is the set of all 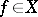 with the property that for each sequence
with the property that for each sequence 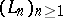 in
in 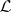 the relations
the relations 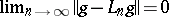 ,
, 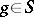 , imply
, imply 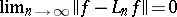 . The problem is to find
. The problem is to find 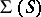 for a given
for a given 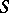 ; if
; if 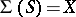 , then
, then 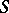 is a Korovkin set (cf. [a1], [a5], [a8]).
is a Korovkin set (cf. [a1], [a5], [a8]).
In some cases one can prove a quantitative form of the Korovkin theorem, estimating the rate of convergence 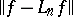 in terms of the rate of convergence for the elements of the Korovkin set. For
in terms of the rate of convergence for the elements of the Korovkin set. For 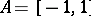 one has obtained estimates in terms of the first- or second-order modulus of continuity
one has obtained estimates in terms of the first- or second-order modulus of continuity 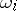 ; for example:
; for example:
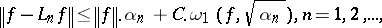 |
with 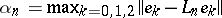 and some constant
and some constant 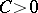 .
.
If some 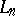 is a polynomial operator, i.e.,
is a polynomial operator, i.e., 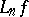 is a polynomial of degree less than or equal to
is a polynomial of degree less than or equal to  , then at least one of the functions
, then at least one of the functions 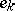 can not be approximated better than
can not be approximated better than 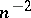 .
.
Similar results can be obtained for 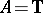 . Also, it is possible to estimate
. Also, it is possible to estimate 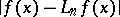 in terms of the moduli of smoothness corresponding to
in terms of the moduli of smoothness corresponding to
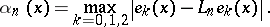 |
Furthermore, quantitative Korovkin theorems for positive linear operators on 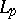 -spaces have been obtained (cf. [a3], [a4]).
-spaces have been obtained (cf. [a3], [a4]).
References
| [a1] | F. Altomare, M. Campiti, "Korovkin-type approximation theory and its applications" , de Gruyter (1994) |
| [a2] | H. Bohman, "On approximation of continuous and of analytic functions" Arkiv. Mat. (2) , 1 (1952) pp. 43–56 |
| [a3] | R.A. DeVore, "The approximation of continuous functions by positive linear operators" , Lecture Notes in Mathematics , 293 , Springer (1972) |
| [a4] | R.A. DeVore, G.G. Lorentz, "Constructive approximation" , Springer (1993) |
| [a5] | K. Donner, "Extension of positive operators and Korovkin theorems" , Lecture Notes in Mathematics , 904 , Springer (1982) |
| [a6] | P.P. Korovkin, "On convergence of linear positive operators in the space of continuous functions" Dokl. Akad. Nauk. SSSR , 90 (1953) pp. 961–964 (In Russian) |
| [a7] | P.P. Korovkin, "Linear operators and approximation theory" , Hindustan Publ. Corp. (1960) (In Russian) |
| [a8] | G.G. Lorentz, M. von Golitschek, Y. Makovoz, "Constructive approximation: advanced problems" , Springer (1996) |
Bohman-Korovkin theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bohman-Korovkin_theorem&oldid=22151