Schubert cell
The orbit of a Borel subgroup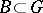 
on a flag variety 
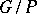[a1], 14.12. Here, 
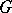is a semi-simple linear algebraic group over an algebraically closed field 
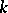and 
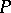is a parabolic subgroup of 
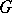so that 
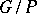is a complete homogeneous variety. Schubert cells are indexed by the cosets of the Weyl group 
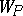of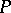 
in the Weyl group 
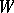of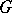 
. Choosing 
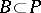, these cosets are identified with 
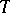-fixed points of 
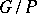, where 
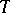is a maximal torus of 
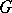and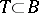 
. The fixed points are conjugates 
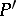of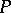 
containing 
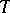. The orbit 
, the affine space of dimension equal to the length of the shortest element of the coset 
. When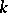 
is the complex number field, Schubert cells constitute a CW-decomposition of 
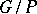(cf. also CW-complex).
Let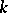 
be any field and suppose 
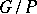is the Grassmannian 
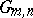of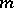 
-planes in 
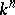(cf. also Grassmann manifold). Schubert cells for 
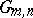arise in an elementary manner. Among the 
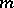by 
matrices whose row space is a given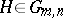 
, there is a unique echelon matrix
 |
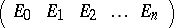where
 |
 |
where 
represents an arbitrary element of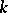 
.
This echelon representative of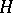 
is computed from any representative by Gaussian elimination (cf. also Elimination theory). The column numbers 
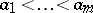of the leading entries (
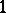s) of the rows in this echelon representative determine the type of 
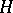. Counting the undetermined entries in such an echelon matrix shows that the set of 
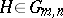with this type is isomorphic to 
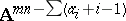. This set is a Schubert cell of 
.
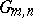References
| [a1] | A. Borel, "Linear algebraic groups" , Grad. Texts Math. , 126 , Springer (1991) (Edition: Second) |
Schubert cell. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schubert_cell&oldid=21929