Representation of a compact group(2)

A homomorphism of a compact group into the group of continuous linear automorphisms of a (complex) Banach space that is continuous with respect to the strong operator topology.

Let be a compact group, let be a Banach space and let be a representation. If is a Hilbert space and is a unitary operator for every , then is called a unitary representation. There always is an equivalent norm in for which is unitary.

Every irreducible unitary representation (cf. Irreducible representation) of a compact group 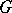is finite-dimensional. Let be the family of all possible pairwise inequivalent irreducible unitary representations of the group 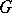. Every unitary representation 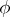of is an orthogonal sum of unique representations , , 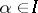such that 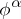is an orthogonal sum, possibly zero, of a set of representations equivalent to .

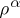If is finite, then the family 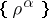is also finite and contains as many elements as there are distinct conjugacy classes in (moreover, ). The problem of studying these representations (computing their characters, finding explicit realizations, etc.) is the subject of an extensive theory (cf. Finite group, representation of a).

If is a connected, simply-connected, compact Lie group and is its complexification (cf. Complexification of a Lie group), then the description of the family for amounts (by restricting the representations to 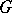) to the description of the family of all irreducible pairwise inequivalent finite-dimensional rational representations of the reductive algebraic group . The latter family, in turn, allows of a complete description by considering highest weights (cf. Representation with a highest weight vector).

In modern number theory and algebraic geometry one considers -adic representations of compact totally-disconnected groups (cf. [5], [6]).

References

[1]	L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian)
[2]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)
[3]	D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian)
[4]	S. Lang, "" , Addison-Wesley (1975)
[5]	I.M. Gel'fand, M.I. Graev, I.I. Pyatetskii-Shapiro, "Generalized functions" , 6. Representation theory and automorphic functions , Saunders (1969) (Translated from Russian)
[6]	J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964)
[7]	C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946)

References

[a1]	N. Bourbaki, "Groupes et algèbres de Lie" , Eléments de mathématiques , Masson (1982) pp. Chapt. 9. Groupes de Lie réels compacts
[a2]	Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985)
[a3]	E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , II , Springer (1970)
[a4]	A. Wawrzyńczyk, "Group representations and special functions" , Reidel & PWN (1984)