Group of finite Morley rank

A group such that the formula has finite Morley rank in the theory . (Cf. also Model theory.) Sometimes 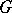appears as a definable group in a structure and in this context is said to have finite Morley rank if the formula defining in has finite Morley rank with respect to the theory of .

There is a well-developed theory of groups of finite Morley rank, both from the model-theoretic and group-theoretic point of view. The theory began with B.I. Zil'ber's study [a4] of groups definable in uncountably categorical structures. G.L. Cherlin's paper [a2] also played an important role in the early theory. Examples of groups of finite Morley rank are algebraic groups over algebraically closed fields (cf. Algebraic group). The Cherlin–Zil'ber conjecture says that any infinite non-commutative simple group of finite Morley rank is an algebraic group over an algebraically closed field. The conjecture remains unproved (1996). A certain amount of the theory of algebraic groups can be developed for groups of finite Morley rank, specifically the notions of generic type, connected component, and stabilizer. Another important technical tool is the Zil'ber indecomposability theorem, which states that if is a group of finite Morley rank and 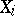, for 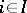, is a family of definable subsets of satisfying some mild assumptions, then the subgroup of 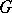generated by all the 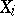is definable and connected. This is an analogue of the Borel theorem for algebraic groups.

The relevance of groups of finite Morley rank for model theory comes from a theorem of Zil'ber which states that if is a model of an uncountably categorical theory (cf. Categoricity in cardinality), then is built up from a set of Morley rank by a finite sequence of "definable fibre bundles" .

Much of the recent work on the Cherlin–Zil'ber conjecture is contained in [a1].

A vast generalization of the theory of groups of finite Morley rank is the theory of stable groups, due essentially to B. Poizat [a3].

References

[a1]	A. Borovik, A. Nesin, "Groups of finite Morley rank" , Oxford Univ. Press (1994)
[a2]	G. Cherlin, "Groups of small Morley rank" Ann. Math. Logic , 17 (1979) pp. 1–28
[a3]	B. Poizat, "Groupes stables" , Nur Al-Mantiq Wal-Ma'rifah, Villeurbanne (1987)
[a4]	B.I. Zil'ber, "Groups and rings whose theory is categorical" Fundam. Math. , 55 (1977) pp. 1730188