Oval

A closed convex 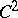-smooth curve in 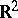. The points of an oval at which the curvature is extremal are called the vertices of the oval. The number of vertices is at least four.

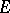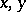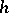Let be an oval, traversed counter-clockwise, in the plane with rectangular Cartesian coordinates ; let be the distance from the origin 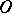to the directed tangent line to 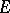( 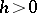if the rotation of the tangent line relative to 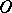is counter-clockwise). Then the equation of the tangent line is

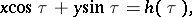where is the angle made by the tangent line and the axis 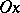. The quantity 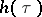is called the support function of the oval. The radius of curvature of the oval is

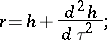and the length of the oval (Cauchy's formula) is

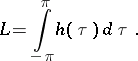The following isoperimetric inequality holds for the length 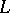and the area 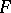of the region inside the oval:

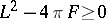(for more details see Bonnesen inequality).

Comments

Sometimes smoothness is not assumed, so that any closed convex curve in 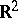is called an oval. In finite (projective) geometry the term "oval" denotes a special kind of ovoid.

References

[a1]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)
[a2]	M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976)
[a3]	S.S. Chern, "Curves and surfaces in Euclidean space" , Prentice-Hall (1967)
[a4]	T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1934)