Stone-Weierstrass theorem

A broad generalization of the classical Weierstrass theorem on the approximation of functions, due to M.H. Stone (1937). Let 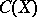be the ring of continuous functions on a compactum 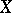with the topology of uniform convergence, i.e. the topology generated by the norm

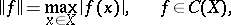and let 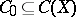be a subring containing all constants and separating the points of 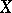, i.e. for any two different points 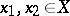there exists a function 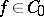for which 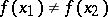. Then 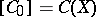, i.e. every continuous function on 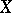is the limit of a uniformly converging sequence of functions in .

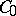Comments

The expository article [a4] is recommended in particular.

References

[a1]	E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982)
[a2]	A. Schönhage, "Approximationstheorie" , de Gruyter (1971)
[a3]	M.H. Stone, "The generalized Weierstrass approximation theorem" Math. Mag. , 21 (1948) pp. 167–183; 237–254
[a4]	M.H. Stone, "A generalized Weierstrass approximation theorem" R.C. Buck (ed.) , Studies in Modern Analysis , 1 , Math. Assoc. Amer. (1962) pp. 30–87
[a5]	M.H. Stone, "Applications of the theory of Boolean rings to general topology" Trans. Amer. Math. Soc. , 41 (1937) pp. 375–481