Maximal term of a series

The term of a convergent series of numbers or functions with positive terms the value of which is not less than the values of all other terms of this series.

Applying this idea to the study of power series

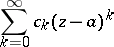in one complex variable with positive radius of convergence , , one has in mind the maximal term of the series

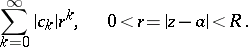Thus,

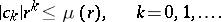The index of the maximal term is called the central index:

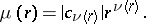If there are several terms in modulus equal to 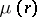, then the central index is taken to be the largest of the indices of these terms. The function

is non-decreasing and convex; the function 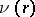is a step-function, increases at discontinuity points in natural numbers and is everywhere continuous from the right.

References

[1]	G. Valiron, "Les fonctions analytiques" , Paris (1954)
[2]	H. Wittich, "Neuere Untersuchungen über eindeutige analytische Funktionen" , Springer (1955)

References

[a1]	G. Pólya, G. Szegö, "Problems and theorems in analysis" , 2 , Springer (1976) pp. Part IV, Chapt. 1 (Translated from German)