Anisotropic group

over a field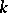

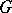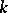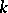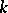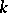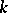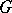A linear algebraic group defined over and of -rank zero, i.e. not containing non-trivial -split tori (cf. Splittable group). Classical examples of anisotropic groups include the orthogonal groups of quadratic forms that do not vanish over ; and algebraic groups of elements of reduced norm one in division algebras over . If is semi-simple, and if the characteristic of 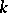is zero, then 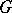is anisotropic over 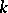if and only if 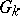contains non-trivial unipotent elements. (For the field of real numbers or the field of 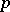-adic numbers this is equivalent to saying that 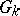is compact.) The classification of arbitrary semi-simple groups over the field 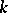reduces essentially to the classification of anisotropic groups.

References

[1]	A. Borel, "Linear algebraic groups" , Benjamin (1969)
[2]	J. Tits, "Classification of algebraic simple groups" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 33–62