Schur stability of polynomials and matrices

Consider the linear discrete-time dynamical system described by the difference equation

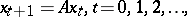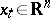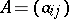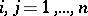where and , , is an 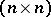-matrix with real coefficients. Let 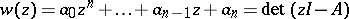be the characteristic polynomial for the dynamical system. The polynomial 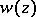(or, equivalently, the matrix 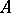) is said to be stable if all its roots are inside the unit circle on the complex plane. Similarly, the dynamical system is said to be asymptotically stable if its characteristic polynomial 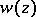is stable [a2].

Asymptotic stability of the polynomial or dynamical system is strongly connected with Schur matrices and Schur's theorem. A Schur matrix is a square matrix with real entries and with eigenvalues (cf. also Eigen value) of absolute value less than one [a1], [a4]. Schur's theorem states that every matrix is unitarily similar to a triangular matrix. It has been noted that the triangular matrix is not unique [a1].

A consequence of this theorem is the following. Let a matrix have eigenvalues . Then

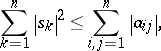with equality if and only if 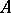is normal (cf. also Normal matrix). This leads to the estimate

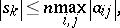which can be directly used in asymptotic stability investigations for the dynamical system.

However, it should be stressed that it is possible to use also a different method in asymptotic stability considerations. Namely, it is possible to associate to the characteristic polynomial 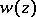the symmetric matrix 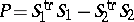, where [a2]:

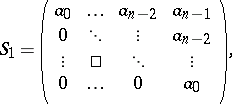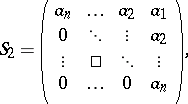and the symbol 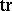denotes transposition. Therefore, the matrix 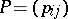, , 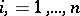where

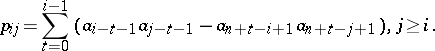The following main stability theorem holds [a2]: The polynomial 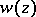is asymptotically stable if and only if the matrix is positive definite, i.e. 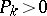for 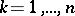, where

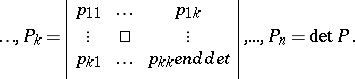Using this theorem, one can prove [a2] that if 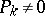for 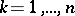, then the characteristic polynomial 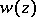has 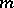roots inside and 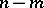roots outside the unit circle, where 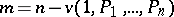and denotes the number of sign changes in the sequence .

Moreover, it should be pointed out that Schur's matrix and Schur's theorem can be also used in the solution of the pole assignment problem for linear control systems [a3].

References

[a1]	R. Bhatia, "Matrix analysis" , Springer (1997)
[a2]	T. Kaczorek, "Theory of control and systems" , PWN (1993) (In Polish)
[a3]	A. Varga, "A Schur method for pole assignment" IEEE Trans. Autom. Control , AC-26 : 2 (1981) pp. 517–519
[a4]	"Comprehensive dictionary of electrical engineering" , CRC (1999) (Dictionary)