Conditional convergence
of a series
A property of series, stating that the given series converges after a certain (possibly trivial) rearrangement of its terms. A series of numbers
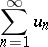 | (*) |
is unconditionally convergent if it converges itself, as well as any series obtained by rearranging its terms, while the sum of any such series is the same; in other words: The sum of an unconditionally-convergent series does not depend on the order of its terms. If the series (*) converges, but not unconditionally, then it is said to be conditionally convergent. For the series (*) to be conditionally convergent it is necessary and sufficient that it converges and does not absolutely converge, i.e. that  .
.
If the terms of the series (*) are real numbers, if the non-negative terms are denoted by  and the negative terms by
and the negative terms by  then the series (*) is conditionally convergent if and only both series
then the series (*) is conditionally convergent if and only both series 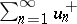 and
and 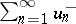 diverge (here the order of the terms in the series is immaterial).
diverge (here the order of the terms in the series is immaterial).
Let the series (*) of real numbers be conditionally convergent and let 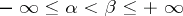 , then there exists a series
, then there exists a series  , obtained by rearranging the terms of (*), such that if
, obtained by rearranging the terms of (*), such that if 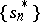 denotes its sequence of partial sums, then
denotes its sequence of partial sums, then
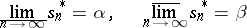 |
(this is a generalization of Riemann's theorem, cf. Riemann theorem 2).
The product of two conditionally-convergent series depends on the order in which the result of the term-by-term multiplication of the two series is summed.
The concepts of conditional and unconditional convergence of series may be generalized to series with terms in some normed vector space 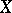 . If
. If 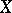 is a finite-dimensional space then, analogously to the case of series of numbers, a convergent series
is a finite-dimensional space then, analogously to the case of series of numbers, a convergent series 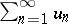 ,
, 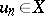 ,
, 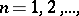 is conditionally convergent if and only if the series
is conditionally convergent if and only if the series 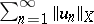 is divergent. If, however,
is divergent. If, however, 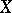 is infinite dimensional, then there exist unconditionally-convergent series
is infinite dimensional, then there exist unconditionally-convergent series 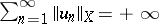 .
.
Comments
A very useful reference on convergence and divergence of series with elements in abstract spaces is [a1].
References
| [a1] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 1. Sequence spaces , Springer (1977) |
| [a2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 107–108 |
Conditional convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conditional_convergence&oldid=19647