Norm-residue symbol

norm residue, Hilbert symbol

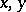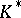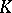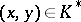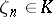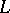A function that associates with an ordered pair of elements of the multiplicative group of a local field an element that is an -th root of unity. This function can be defined as follows. Let be a primitive -th root of unity. The maximal Abelian extension of 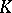with Galois group of exponent is obtained by adjoining to 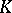the roots 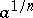for all . On the other hand, there is a canonical isomorphism (the fundamental isomorphism of local class field theory)

The norm residue of the pair 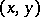is defined by

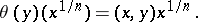D. Hilbert introduced the concept of a norm-residue symbol in the special case of quadratic fields with 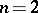. In [4] there is an explicit definition of the norm residue using only local class field theory.

Properties of the symbol :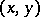

1) bilinearity: , ;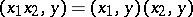

2) skew-symmetry: ;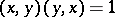

3) non-degeneracy: 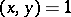for all 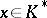implies 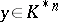; 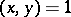for all 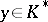implies ;

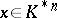4) if 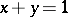, then ;

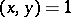5) if 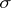is an automorphism of 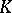, then

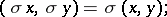6) let 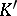be a finite extension of , 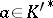and 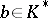. Then

where on the left-hand side the norm-residue symbol is regarded for 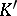and on the right-hand side that for 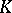, and where 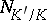is the norm map from 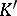into ;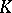

7) 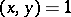implies that 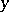is a norm in the extension 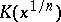. (This explains the name of the symbol.)

The function 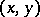induces a non-degenerate bilinear pairing

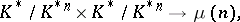where 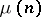is the group of roots of unity generated by 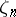. Let 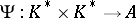be a mapping into some Abelian group satisfying 1), 4) and the condition of continuity: For any 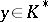the set 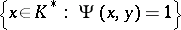is closed in . The norm-residue symbol has the following universal property [3]: If is the number of roots of unity in 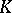, then there exists a homomorphism 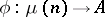such that for any ,

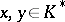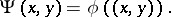This property can serve as a basic axiomatic definition of the norm-residue symbol.

If 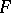is a global field and 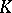is the completion of 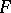relative to a place , then by the norm-residue symbol one also means the function 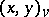defined over 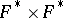that is obtained by composition of the (local) norm-residue symbol 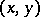with the natural imbedding .

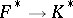Often the norm-residue symbol is defined as an automorphism 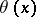of the maximal Abelian extension of 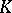corresponding to an element by local class field theory.

References

[1]	J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986)
[2]	H. Koch, "Galoissche Theorie der 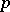-Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970)
[3]	J.W. Milnor, "Introduction to algebraic 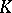-theory" , Princeton Univ. Press (1971)
[4]	I.R. Shafarevich, "A general reciprocity law" Mat. Sb. , 26 : 1 (1950) pp. 113–146 (In Russian)

References

[a1]	K. Iwasawa, "Local class field theory" , Oxford Univ. Press (1986)
[a2]	J. Neukirch, "Class field theory" , Springer (1986) pp. Chapt. 4, Sect. 8