Hasse invariant

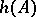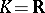The Hasse invariant of a central simple algebra over a local field (or over the field or 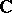) is the image of the class of 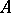under the canonical isomorphism of the Brauer group of 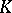onto the group of all complex roots of unity (or onto the group 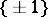or 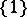). For a cyclic algebra 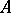with generators 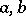and defining relations 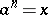, , 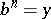, 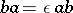where 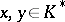and 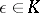is a primitive -th root of unity, the Hasse invariant 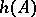is the same as the norm-residue symbol (Hilbert symbol) 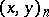. In particular, the Hasse invariant of the quaternion algebra is .

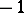For a central algebra 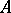over a global field and any valuation of this field the local Hasse invariant 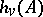is defined as the Hasse invariant of the algebra 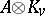over the completion 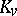of 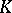in the topology determined by . The local Hasse invariants determine the class of 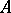uniquely. They are related by the following conditions: 1) there are only finitely-many valuations for which 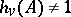; and 2) 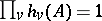(the reciprocity law). Apart from these conditions they can assume arbitrary values.

The Hasse invariant was introduced by H. Hasse [1] and [2].

References

[1]	H. Hasse, "Ueber 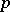-adische Schiefkörper und ihre Bedeutung für die Arithmetik hyperkomplexen Zahlsysteme" Math. Ann. , 104 (1931) pp. 495–534
[2]	H. Hasse, "Die Struktur der R. Brauerschen Algebrenklassengruppe über einem algebraischen Zahlkörper. Inbesondere Begründung der Theorie des Normenrestsymbols und Herleitung des Reziprozitätsgesetzes mit nichtkommutativen Hilfsmitteln" Math. Ann. , 107 (1933) pp. 731–760
[3]	J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986)
[4]	A. Weil, "Basic number theory" , Springer (1967)

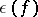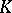The Hasse invariant, the Hasse–Minkowski invariant, Hasse's symbol, , of a non-degenerate quadratic form over a local field of characteristic 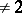(or over the field 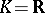or 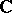) is the product

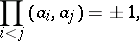where 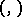is the quadratic Hilbert symbol, that is, 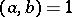if the quadratic form 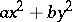represents 1 in the fiel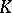d and 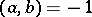otherwise. The Hasse invariant depends only on the equivalence class of the form 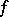, and not on the choice of a diagonal form in this class. Sometimes the Hasse invariant is defined as the product 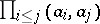, which differs from the definition above by the factor 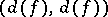, where 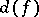is the discriminant of the form .

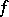In the case of a local field 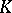the number of variables, the discriminant and the Hasse invariant determine the class of the form 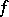. For 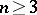, the invariants 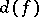and 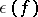can take arbitrary values independently of each other; for 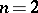the case 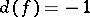, 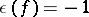is excluded; for 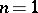one always has .

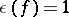When 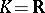, the Hasse invariant can be expressed in terms of the signature, namely,

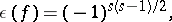where is the negative index of inertia of the form 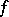. When 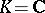, one has .

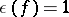For a non-degenerate quadratic form 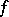over a global field 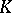of characteristic 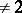and any valuation of 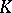the local Hasse invariant 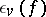is defined as the Hasse invariant of the quadratic form 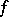regarded over the completion 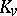of 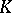in the topology determined by . The number of variables, the discriminant, the local Hasse invariants, and the signatures over the real completions of 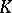determine the class of .

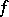Necessary and sufficient conditions for the existence of a non-degenerate quadratic form in variables over a global field 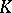of characteristic 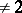having a given discriminant 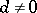, given the local Hasse invariants 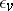, and, for real valuations , given the negative indices of inertia 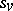, are as follows:

a) 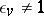for only finitely-many valuations ;

b) 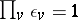(a consequence of the quadratic reciprocity law);

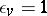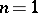c) if or if 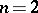and ;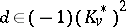

d) 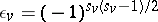for every real valuation ;

e) 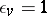for every complex valuation ;

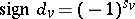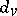f) for every real valuation (here is the image of 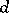under the isomorphism ).

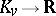The Hasse invariant was introduced by H. Hasse .

References

[1a]	H. Hasse, "Ueber die Darstellbarkeit von Zahlen durch quadratische Formen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 152 (1923) pp. 129–148
[1b]	H. Hasse, "Ueber die Aequivalenz quadratischer Formen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 152 (1923) pp. 205–224
[1c]	H. Hasse, "Symmetrische Matrizen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 153 (1924) pp. 12–43
[1d]	H. Hasse, "Darstellbarkeit von Zahlen durch quadratische Formen in einem beliebigen algebraischen Zahlkörper" J. Reine Angew. Math. , 153 (1924) pp. 113–130
[1e]	H. Hasse, "Aequivalenz quadratischer Formen in einem beliebigen algebraischen Zahlkörper" J. Reine Angew. Math. , 153 (1924) pp. 158–162
[2]	O.T. O'Meara, "Introduction to quadratic forms" , Springer (1963)
[3]	T.Y. Lam, "The algebraic theory of quadratic forms" , Benjamin (1973)
[4]	J.W.S. Cassels, "Rational quadratic forms" , Acad. Press (1978)

The Hasse invariant of an elliptic curve 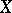over a field 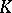of characteristic 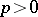is the number 0 or 1 depending on whether the endomorphism of the cohomology group 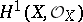induced by the Frobenius endomorphism of 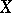is null or bijective. Curves for which the Hasse invariant is zero are called supersingular.

References

[1]	R. Hartshorne, "Algebraic geometry" , Springer (1977)
[2]	Yu.I. Manin, "On the Hasse–Witt matrix of an algebraic curve" Izv. Akad. Nauk. SSSR Ser. Mat. , 25 : 1 (1961) pp. 153–172 (In Russian)

References

[a1]	J.H. Silverman, "The arithmetic of elliptic curves" , Springer (1986)