Component of a space
From Encyclopedia of Mathematics
A connected subset \(C\) of a topological space \(X\) with the following property: If \(C_1 \subset X\) is a connected subset such that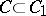 
, then 
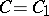. The components of a space are disjoint. Every non-empty connected subset is contained in exactly one component. If \(C\) is a component of a space \(X\) and 
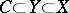, then 
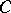is a component of 
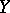. If 
is a monotone continuous mapping onto, then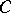 
is a component of 
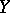if and only if 
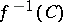is a component of 
.
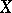References
| [1] | K. Kuratowski, "Topology" , 2 , Acad. Press (1968) (Translated from French) |
How to Cite This Entry:
Component of a space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Component_of_a_space&oldid=19330
Component of a space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Component_of_a_space&oldid=19330
This article was adapted from an original article by B.A. Efimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article