Symmetric algebra

A generalization of a polynomial algebra. If $M$ is a unital module over a commutative associative ring $A$ with an identity, then the symmetric algebra of $M$ is the algebra $S(M) = T(M)/I$, where $T(M)$ is the tensor algebra of $M$ and $I$ is the ideal generated by the elements of the form $x \otimes y - y \otimes x$ ($x,y \in M$). A symmetric algebra is a commutative associative $A$-algebra with an identity. It is graded: $$S(M) = \bigoplus_{p \ge 0} S^p(M)$$ where $S^p(M) = T^p(M)/(T^p(M)\cap I)$, and $S^0(M) = A$, $S^1(M) = M$. The module $S^p(M)$ is called the $p$-th symmetric power of the module $M$. If $M$ is a free module with finite basis $x_1,\ldots,x_n$, then the correspondence $x_i \mapsto X_i$ ($i=1,\ldots,n$) extends to an isomorphism of $S(M)$ onto the polynomial algebra $A[X_1,\ldots,X_n]$ (see Ring of polynomials).

For any homomorphism $f:M \to N$ of $A$-modules, the $p$-th tensor power $T^p(f)$ induces a homomorphism $S^p(f) : S^p(M) \to S^p(N)$ (the $p$-th symmetric power of the homomorphism $f$). A homomorphism $S(f) : S(M) \to S(N)$ of $A$-algebras is obtained. The correspondences $f \mapsto S^p(f)$ and $f \mapsto S(f)$ are, respectively, covariant functors from the category of $A$-modules into itself and into the category of $A$-algebras. For any two $A$-modules $M$ and $N$ there is a natural isomorphism $S(M\oplus N) = S(M) \otimes_A S(N)$. If 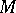is a vector space over a field of characteristic 0, then the symmetrization 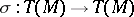(cf. Symmetrization (of tensors)) defines an isomorphism from the symmetric algebra 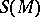onto the algebra 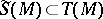of symmetric contravariant tensors over 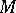relative to symmetric multiplication:

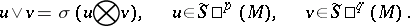References

[1]	N. Bourbaki, "Eléments de mathématique" , 2. Algèbre , Hermann (1964) pp. Chapt. IV-VI
[2]	A.I. Kostrikin, Yu.I. Manin, "Linear algebra and geometry" , Gordon & Breach (1989) (Translated from Russian)

Comments

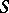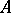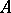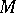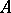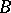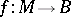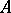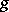The functor from -modules to commutative unitary -algebras solves the following universal problem. Let be an -module and a commutative unitary -algebra. For each homomorphism of -modules there is a unique homomorphism of -algebras such that restricted to 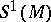coincides with 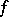. Thus, 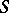is a left-adjoint functor of the underlying functor from the category of commutative unitary 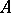-algebras to the category of 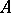-modules.