Co-algebra

A module $A$ over a commutative ring $k$ with two homomorphisms $\phi$ and $\epsilon$ such that the diagrams $$ \begin{array}{ccc} A & \stackrel{\phi}{\rightarrow} & A \otimes A \\ \phi\,\downarrow & \ & \downarrow\,1 \otimes \phi \\ A \otimes A & \stackrel{\phi \otimes 1}{\longrightarrow} & A \otimes A \end{array} $$ and $$ \begin{array}{ccccc} A \otimes A & \stackrel{\phi}{\leftarrow} & A & \stackrel{\phi}{\rightarrow} & A \otimes A \\ & \searrow\,\epsilon\otimes1\ & & 1\otimes\epsilon\,\swarrow & \\ & & A & & \end{array} $$ are commutative. In other words, a co-algebra is the dual concept (in the sense of category theory) to the concept of an associative algebra over a ring .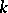

Co-algebras have acquired significance in connection with a number of topological applications such as, for example, the simplicial complex of a topological space, which is a co-algebra. Closely related to co-algebras are the Hopf algebras, which possess algebra and co-algebra structures simultaneously (cf. Hopf algebra).

References

[1]	S. MacLane, "Homology" , Springer (1963)

Comments

Given a co-algebra $A$ over $k$, let $A^*$ be the module of $k$-module homomorphisms from $A$ to $k$. For $f,g \in A^*$ define the product $fg : A \to k$ by the formula $fg : a \mapsto (f\otimes g)(\phi(a))$, where $k \otimes_k k$ is identified with $k$. For any two $k$-modules $M,N$ define $\rho : M^* \otimes N^* \to (M \otimes N)^*$ by $\rho(f\otimes g)(m\otimes n) = f(m)g(n)$. Then the multiplication on $A^*$ can also be seen as the composite $A^* \otimes A^* \to (A\otimes A)^* \stackrel{\phi^*}{\to} A^*$. The element $\epsilon : A \to k$ is a unit element for this multiplication making $A^*$ an associative algebra with unit, the dual algebra. In general the mapping $\rho$ is not an isomorphism and there is no natural $k$-module homomorphism $M^* \otimes N^* \to (M \otimes N)^*$. Thus there is no equally natural construction associating a co-algebra to an algebra over $k$, even when $k$ is a field. In that case there does however exist an adjoint functor $A \mapsto A^0$ to the functor $C \to C^*$ which associates to a co-algebra its dual algebra, i.e. 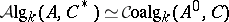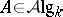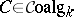for , , where 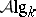and 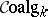denote, respectively, the category of 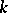-algebras and the category of 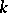-co-algebras, [a2]; cf. also Hopf algebra. But if 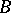is free of finite rank over 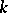then 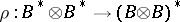is an isomorphism and the dual co-algebra can be defined.

Let 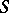be the s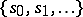et . Let 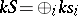and define

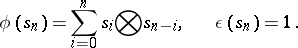Then 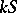is a co-algebra.

If 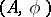and 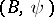are two co-algebras, then a morphism of co-algebras is a 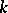-module morphism 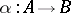such that 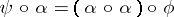and 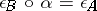. A co-ideal of a co-algebr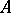a is a 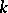-submodule 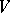such that 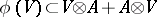and .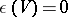

A co-module 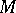over a co-algebr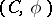a is a 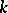-module with a 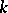-module morphism 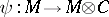such that 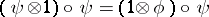and 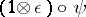the canonical isomorphism 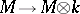. There are obvious notions of homomorphisms of co-modules, etc.

References

[a1]	M. Sweedler, "Hopf algebras" , Benjamin (1969)
[a2]	E. Abe, "Hopf algebras" , Cambridge Univ. Press (1980)