Motzkin transposition theorem

The thesis of T.S. Motzkin, [a6], in particular his transposition theorem, was a milestone in the development of linear inequalities and related areas.

For two vectors $\mathbf{u} = (u_i)$ and $\mathbf{v} = (v_i)$ of equal dimension one denotes by $\mathbf{u}\geq\mathbf{v}$ and $\mathbf{u}>\mathbf{v}$ that the indicated inequality holds componentwise, and by $\mathbf{u}\gneq\mathbf{v}$ the fact $\mathbf{u}\geq\mathbf{v}$ and $\mathbf{u}\neq\mathbf{v}$.

Systems of linear inequalities appear in several forms; the following examples are typical:

1. a) $A\mathbf{x}\leq\mathbf{b}$;
2. b) $A\mathbf{x}=\mathbf{b}$, $\mathbf{x}\geq\mathbf{0}$;
3. c) $A\mathbf{x}\leq\mathbf{b}$, $B\mathbf{x}<\mathbf{c}$;
4. d) $A\mathbf{x}=\mathbf{0}$, $\mathbf{x}\gneq\mathbf{0}$;
5. e) $A\mathbf{x}=\mathbf{0}$, $\mathbf{x}>\mathbf{0}$;
6. f) $A\mathbf{x}>\mathbf{0}$, $B\mathbf{x}\geq\mathbf{0}$, $C\mathbf{x}=\mathbf{0}$.

In each of these so-called primal systems the existence of solutions is characterized by means of a dual system, using the transposes of matrices in the primal system. Hence the name "transposition theorem" . The relation between the primal and dual systems is sometimes given as a "theorem of alternatives" , listing alternatives, i.e. statements $P$, $Q$ satisfying $P\Leftrightarrow\neg Q$ (where $\neg$ denotes negation), in words: either $P$ or $Q$ but never both.

Relations between a)–f).

a) and b) are equivalent representations. Indeed, they can be written as \begin{equation} (A, -A, I) \begin{pmatrix} \mathbf{x}^+ \\ \mathbf{x}^- \\ \mathbf{s} \end{pmatrix} = \mathbf{b} \quad\text{and}\quad \begin{pmatrix} \mathbf{x}^+ \\ \mathbf{x}^- \\ \mathbf{s} \end{pmatrix} \geq \mathbf{0}, \end{equation} \begin{equation} \begin{pmatrix} A \\ -A \\ -I \end{pmatrix}\mathbf{x}\leq\begin{pmatrix} \mathbf{b} \\ -\mathbf{b} \\ \mathbf{0} \end{pmatrix},\end{equation} respectively.

The remaining systems involve strict inequalities or non-trivial solutions. For example, d) and e) concern the existence of non-trivial solutions and positive solutions, respectively, for the system \begin{equation} A\mathbf{x}=\mathbf{0}, \;\mathbf{x}\geq\mathbf{0}. \end{equation}

Taking $B=0$ and $\mathbf{c}>\mathbf{0}$ in c) gives a), showing that a) and b) are special cases of c). Similarly, the systems d) and e) are special cases of f), which itself is a special case of c) with $\mathbf{b}=\mathbf{0}$, $\mathbf{c}=\mathbf{0}$. In fact, every system of linear inequalities can be written as c).

The following two versions of Motzkin's transposition theorem, [a6], concern systems c) and f):

(solvability of c)) Given matrices 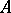, 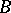and vectors 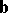, , the following are equivalent:

c1) the system 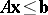, 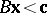has a solution ;

c2) for all vectors , ,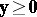

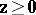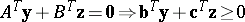and

(solvability of f)) Let , , be given matrices, with 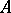non-vacuous. Then the following are alternatives:

f1) 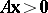, , 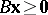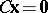has a solution ;

f2) 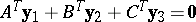, , 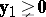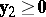has solutions , , .

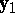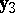Special cases of Motzkin's theorem include the following theorems.

Farkas theorem.

(See also [a2].) Let 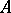be a given matrix and 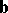a given vector.

Farkas' theorem for system a) says that the following are equivalent:

a1) the system 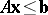has a solution ;

a2) , .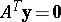

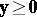
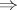
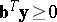Farkas' theorem for system b) says that the following are equivalent:

b1) the system 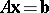, 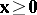has a solution ;

b2) .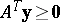

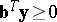The positively homogeneous systems d) and e) are covered by the following two theorems.

Gordan's theorem.

(See also [a3].) Given a matrix , the following are alternatives:

d1) 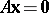, has a solution ;

d2) has a solution .

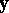Stiemke's theorem.

(See also [a9].) Given a matrix 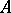, the following are alternatives:

e1) , 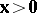has a solution ;

e2) 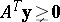has a solution .

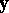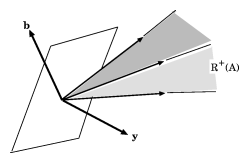
Figure: m130240a

A hyperplane with normal separating 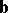and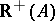

Figure: m130240b

Illustration of the alternatives (a6): ,

Separation theorems.

The above results are separation theorems, or statements about the existence of hyperplanes separating certain disjoint convex sets. First, some terminology. A set 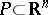is polyhedral (and necessarily convex) if it is the intersection of finitely many closed half-spaces, say

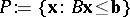(a1)

A finitely generated cone is the set of non-negative linear combinations of finitely many vectors (generators). An example is the cone generated by the columns of a matrix :

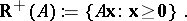(a2)

The dual (or polar) of a non-empty set is defined as

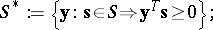(a3)

it is a closed convex cone. In particular,

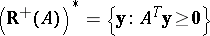(a4)

is a polyhedral cone. Farkas' theorem b1) states that the vector is in the cone 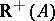. The equivalent statement b2) says that 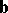cannot be separated from 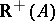by a hyperplane: such a separating hyperplane would have a normal 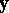satisfying

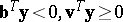for all 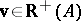(see e.g. Fig.a1), which by (a4) is a negation of b2). Farkas' theorem for system b) states that for any matrix ,

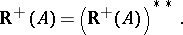(a5)

In general, a set 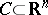is a closed convex cone if and only if . Farkas' theorem for system b) also implies that a cone in 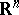is polyhedral if and only if it is finitely generated (the Farkas–Minkowski–Weyl theorem, [a8], Corol. 7.1a). More generally, a set 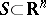is polyhedral if and only if it is the sum of a finitely generated cone and the convex hull of finitely many points (the Minkowski–Steinitz–Weyl theorem, [a8], Corol. 7.1b).

The theorems of Stiemke and Gordan can be interpreted as geometric statements about intersections 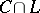of a pointed closed convex cone 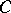and a subspace 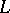in . Let 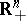denote the non-negative orthant in .

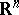Thus, Gordan' theorem d1) says that 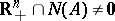, where 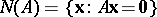is the null space of . And Stiemke's theorem e1) says that 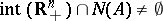, where .

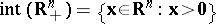In each case, the dual system uses the intersection 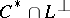, where 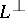is the orthogonal complement of 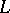. For example, the statements

(a6)

are mutually exclusive (see e.g. Fig.a2), for otherwise

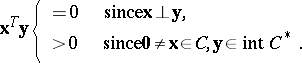To make the statements in (a6) alternatives, one has to show that one of them occurs, the hard part of the proof. Returning to the theorems of Gordan and Stiemke, recall that 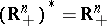and 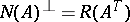. Then Gordan's theorem d1), 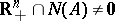, and d2), 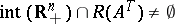, are alternatives.

Likewise, Stiemke's theorems e1), 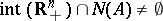, and e2), , are alternatives.

For history, see [a8], pp. 209–228. For theorems of alternatives, see [a5], pp. 27–37. Generalizations can be found in [a10], [a1], [a11], Sec. 21–22, especially Thm. 21.1; 22.6. Finally, see [a7], [a5], p.100, for applications.

References

[a1]	K. Fan, "Systems of linear inequalities" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Linear Inequalities and Related Systems , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956,}) pp. 99–156
[a2]	J. Farkas, "Über die Theorie der einfachen Ungleichungen" J. Reine Angew. Math. , 124 (1902) pp. 1–24
[a3]	P. Gordan, "Über die Auflösungen linearer Gleighungen mit reelen Coefficienten" Math. Ann. , 6 (1873) pp. 23–28
[a4]	"Linear inequalities and related systems" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956)
[a5]	O.L. Mangasarian, "Nonlinear programming" , McGraw-Hill (1969)
[a6]	T.S. Motzkin, "Beiträge zur Theorie der linearen Ungleichungen" Inaugural Diss. (Basel, Jerusalem) (1936)
[a7]	T.S. Motzkin, "Two consequences of the transposition theorem on linear inequalities" Econometrica , 19 (1951) pp. 184–185
[a8]	A. Schrijver, "Theory of linear and integer programming" , Wiley/Interscience (1986)
[a9]	E. Stiemke, "Über positive Lösungen homogener linearer Gleichungen" Math. Ann. , 76 (1915) pp. 340–342
[a10]	A.W. Tucker, "Dual systems of homogeneous linear relations" H.W. Kuhn (ed.) A.W. Tucker (ed.) , Linear Inequalities and Related Systems , Ann. of Math. Stud. , 38 , Princeton Univ. Press (1956) pp. 3–18
[a11]	R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970)