Riemann integral

A generalization of the concept of a Cauchy integral to a certain class of discontinuous functions; introduced by B. Riemann (1853). Consider a function $f$ which is given on an interval $[a,b]$. Let $a=x_0<x_1<\dots<x_n=b$ is a partition (subdivision) of the interval $[a,b]$ and $\Delta x_i = x_i-x_{i-1}$, where $i=1,\dots,n$. The sum \begin{equation}\label{eq:1} \sigma = f(\xi_1)\Delta x_1+\dots+f(\xi x_i)\Delta x_i +\dots +f(x_n)\Delta x_n, \end{equation} where $x_{i-1}\leq\xi_i\leq x_i$, is called the Riemann sum corresponding to the given partition of $[a,b]$ by the points $x_i$ and to the sample of points $\xi_i$. The number $I$ is called the limit of the Riemann sums \ref{eq:1} as $\max_i \Delta x_i \to 0$ if for any $\varepsilon>0$ a $\delta>0$ can be found such that $\max_i \Delta x_i < \delta$ implies the inequality $|\sigma - I|<\varepsilon$. If the Riemann sums have a finite limit $I$ as $\max_i \Delta x_i \to 0$, then the function $f$ is called Riemann integrable over $[a,b]$, where $a<b$. The limit is known as the definite Riemann integral of $f$ over $[a,b]$, and is written as

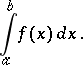(2)

When 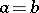then, by definition,

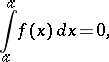and when 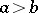the integral (2) is defined using the equation

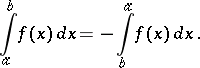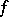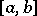A necessary and sufficient condition for the Riemann integrability of over is the boundedness of 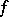on this interval and the zero value of the Lebesgue measure of the set of all points of discontinuity of 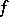contained in .

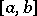Properties of the Riemann integral.

1) Every Riemann-integrable functi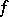on on 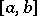is also bounded on this interval (the converse is not true: The Dirichlet function is an example of a bounded and non-integrable function on ).

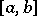2) The linearity property: For any constants 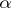and 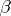, the integrability over 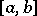of both functions 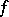and 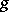implies that the function 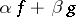is integrable over this interval, and the equation

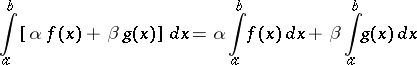holds.

3) The integrability over 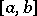of both functions 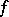and 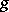implies that their product 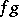is integrable over this interval.

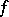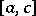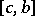4) Additivity: The integrability of a function over both intervals and implies that 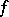is integrable over 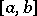, and

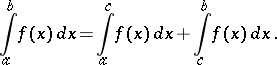5) If two functions 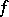and 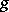are integrable over 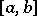and if 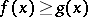for every in this interval, then

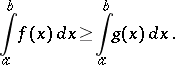6) The integrability of a function 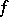over 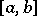implies that the function 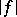is integrable over this interval, and the estimate

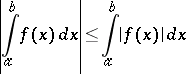holds.

7) The mean-value formula: If two real-valued functions 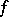and 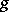are integrable over 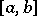, if the function 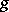is non-negative or non-positive everywhere on this interval, and if 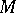and 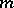are the least upper and greatest lower bounds of 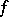on 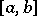, then a number 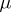can be found, 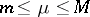, such that the formula

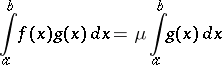(3)

holds. If, in addition, 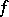is continuous on 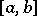, then this interval will contain a point 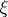such that in formula (3),

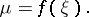8) The second mean-value formula (Bonnet's formula): If a function 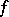is real-valued and integrable over 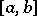and if a function 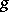is real-valued and monotone on this interval, then a point 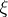can be found in 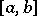such that the formula

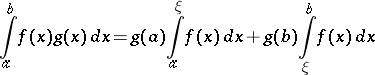holds.

References

[1]	B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" H. Weber (ed.) , B. Riemann's Gesammelte Mathematische Werke , Dover, reprint (1953) pp. 227–271 ((Original: Göttinger Akad. Abh. (1868)))
[2]	V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian)
[3]	L.D. Kudryavtsev, "A course in mathematical analysis" , 1–2 , Moscow (1988) (In Russian)
[4]	S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian)

References

[a1]	G.E. Shilov, "Mathematical analysis" , 1–2 , M.I.T. (1974) (Translated from Russian)
[a2]	I.N. Pesin, "Classical and modern integration theories" , Acad. Press (1970) (Translated from Russian)
[a3]	K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981)
[a4]	W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 75–78