Non-Abelian cohomology
Cohomology with coefficients in a non-Abelian group, a sheaf of non-Abelian groups, etc. The best known examples are the cohomology of groups, topological spaces and the more general example of the cohomology of sites (i.e. topological categories; cf. Topologized category) in dimensions 0, 1. A unified approach to non-Abelian cohomology can be based on the following concept. Let $ C ^{0} $,
$ C ^{1} $
be groups, let $ C ^{2} $
be a set with a distinguished point $ e $,
let $ \mathop{\rm Aff}\nolimits \ C ^{1} $
be the holomorph of $ C ^{1} $(
i.e. the semi-direct product of $ C ^{1} $
and $ \mathop{\rm Aut}\nolimits ( C ^{1} ) $;
cf. also Holomorph of a group), and let $ \mathop{\rm Aut}\nolimits \ C ^{2} $
be the group of permutations of $ C ^{2} $
that leave $ e $
fixed. Then a non-Abelian cochain complex is a collection $$
C ^{*} = (C ^{0} ,\ C ^{1} ,\ C ^{2} ,\ \rho ,\
\sigma ,\ \delta ),
$$
where $ \rho : \ C ^{0} \rightarrow \mathop{\rm Aff}\nolimits \ C ^{1} $,
$ \sigma : \ C ^{0} \rightarrow \mathop{\rm Aut}\nolimits \ C ^{2} $
are homomorphisms and $ \delta : \ C ^{1} \rightarrow C ^{2} $
is a mapping such that $$
\delta (e) = e
\textrm{ and }
\delta ( \rho (a) b) = \sigma (a) \delta (b),
a \in C ^{0} , b \in C ^{1} .
$$
Define the $ 0 $-
dimensional cohomology group by $$
H ^{0} (C ^{*} ) = \rho ^{-1} ( \mathop{\rm Aut}\nolimits \ C ^{1} ),
$$
and the $ 1 $-
dimensional cohomology set (with distinguished point) by $$
H ^{1} (C ^{*} ) = Z ^{1} / \rho ,
$$
where $ Z ^{1} = \delta ^{-1} (e) \subseteq C ^{1} $
and the factorization is modulo the action $ \rho $
of the group $ C ^{0} $.
Examples.
1) Let $ X $ be a topological space with a sheaf of groups $ {\mathcal F} $, and let $ \mathfrak U $ be a covering of $ X $; one then has the Čech complex $$ C ^{*} ( \mathfrak U ,\ {\mathcal F} ) = (C ^{0} ( \mathfrak U ,\ {\mathcal F} ), C ^{1} ( \mathfrak U ,\ {\mathcal F} ), C ^{2} ( \mathfrak U ,\ {\mathcal F} )), $$ where $ C ^{i} ( \mathfrak U ,\ {\mathcal F} ) $ are defined as in the Abelian case (see Cohomology), $$ ( \sigma (a) (c)) _{ijk} = a _{i} c _{ijk} a _{i} ^{-1} , $$ $$ ( \delta b) _{ijk} = b _{ij} b _{jk} b _{ik} ^{-1} , $$ $$ a \in C ^{0} , b \in C ^{1} , c \in C ^{2} . $$ Taking limits with respect to coverings, one obtains from the cohomology sets $ H ^{i} (C ^{*} ( \mathfrak U ,\ {\mathcal F} )) $, $ i = 0,\ 1 $, the cohomology $ H ^{i} (X,\ {\mathcal F} ) $, $ i = 0,\ 1 $, of the space $ X $ with coefficients in $ {\mathcal F} $. Under these conditions, $ H ^{0} (X,\ {\mathcal F} ) = {\mathcal F} (X) $. If $ {\mathcal F} $ is the sheaf of germs of continuous mappings with values in a topological group $ G $, then $ H ^{1} (X,\ {\mathcal F} ) $ can be interpreted as the set of isomorphism classes of topological principal bundles over $ X $ with structure group $ G $. Similarly one obtains a classification of smooth and holomorphic principal bundles. In a similar fashion one defines the non-Abelian cohomology for a site; for an interpretation see Principal $ G $- object.
2) Let $ G $ be a group and let $ A $ be a (not necessarily Abelian) $ G $- group, i.e. an operator group with group of operators $ G $. Denote the action of an operator $ g \in G $ on an element $ a \in A $ by $ a ^{g} $. Define a complex $ C ^{*} (G,\ A) $ by the formulas $$ C ^{k} = \mathop{\rm Map}\nolimits (G ^{k} ,\ A), k = 0,\ 1,\ 2, $$ $$ ( \rho (a) (b)) (g) = ab (g) (a ^{g} ) ^{-1} , $$ $$ ( \sigma (a) (c)) (g,\ h) = a ^{g} c (g,\ h) (a ^{g} ) ^{-1} , $$ $$ \delta (b) (g,\ h) = b (g) ^{-1} b (gh) (b (h) ^{g} ) ^{-1} , $$ $$ a \in C ^{0} , b \in C ^{1} , c \in C ^{2} , g \in G. $$ The group $ H ^{0} (G,\ A) = H ^{0} (C ^{*} (G,\ A)) $ is the subgroup $ A ^{G} $ of $ G $- fixed points in $ A $, while $ H ^{1} (G,\ A) = H ^{1} ( C ^{*} ( G ,\ A ) ) $ is the set of equivalence classes of crossed homomorphisms $ G \rightarrow A $, interpreted as the set of isomorphism classes of principal homogeneous spaces (cf. Principal homogeneous space) over $ A $. For applications and actual computations of non-Abelian cohomology groups see Galois cohomology. Analogous definitions yield the non-Abelian cohomology of categories and semi-groups.
3) Let $ X $ be a smooth manifold, $ G $ a Lie group and $ \mathfrak g $ the Lie algebra of $ G $. The non-Abelian de Rham complex $ R _{G} ^{*} (X) $ is defined as follows: $ R _{G} ^{0} (X) $ is the group of all smooth functions $ X \rightarrow G $; $ R _{G} ^{k} (X) $, $ k = 1,\ 2 $, is the space of exterior $ k $- forms on $ X $ with values in $ \mathfrak g $; $$ \rho (f \ ) ( \alpha ) = df \cdot f ^ {\ -1} + ( \mathop{\rm Ad}\nolimits \ f \ ) \alpha ; $$ $$ \sigma (f \ ) ( \beta ) = ( \mathop{\rm Ad}\nolimits \ f \ ) \beta , $$ $$ \delta \alpha = d \alpha - { \frac{1}{2} } [ \alpha ,\ \alpha ], $$ $$ f \in R _{G} ^{0} , a \in R _{G} ^{1} , \beta \in R _{G} ^{2} . $$ The set $ H ^{1} (R _{G} (X)) $ is the set of classes of totally-integrable equations of the form $ df \cdot f ^ {\ -1} = \alpha $, $ \alpha \in R _{G} ^{1} $, modulo gauge transformations. An analogue of the de Rham theorem provides an interpretation of this set as a subset of the set $ H ^{1} ( \pi _{1} (M),\ G) $ of conjugacy classes of homomorphisms $ \pi _{1} (M) \rightarrow G $. In the case of a complex manifold $ M $ and a complex Lie group $ G $, one again defines a non-Abelian holomorphic de Rham complex and a non-Abelian Dolbeault complex, which are intimately connected with the problem of classifying holomorphic bundles [3]. Non-Abelian complexes of differential forms are also an important tool in the theory of pseudo-group structures on manifolds.
For each subcomplex of a non-Abelian cochain complex there is an associated exact cohomology sequence. For example, for the complex $ C ^{*} (G,\ A) $ of Example 2 and its subcomplex $ C ^{*} (G,\ B) $, where $ B $ is a $ G $- invariant subgroup of $ A $, this sequence is $$ e \rightarrow H ^{0} (G,\ B) \rightarrow H ^{0} (G,\ A) \rightarrow (A/B) ^{G } \rightarrow $$ $$ \rightarrow H ^{1} (G,\ B) \rightarrow H ^{1} (G,\ A). $$ If $ B $ is a normal subgroup of $ A $, the sequence can be continued up to the term $ H ^{1} (G,\ A/B) $, and if $ B $ is in the centre it can be continued to $ H ^{2} (G,\ B) $. This sequence is exact in the category of sets with a distinguished point. In addition, a tool is available ( "twisted" cochain complexes) for describing the pre-images of all — not only the distinguished — elements (see [1], [6], [3]). One can also construct a spectral sequence related to a double non-Abelian complex, and the corresponding exact boundary sequence.
Apart from the 0- and $ 1 $- dimensional non-Abelian cohomology groups just described, there are also $ 2 $- dimensional examples. A classical example is the $ 2 $- dimensional cohomology of a group $ G $ with coefficients in a group $ A $; the definition is as follows. Let $ {\mathcal Z} ^{2} (G,\ A) $ denote the set of all pairs $ (m,\ \phi ) $, where $ m: \ G \times G \rightarrow A $, $ \phi : \ G \rightarrow \mathop{\rm Aut}\nolimits \ A $ are mappings such that $$ \phi (g _{1} ) \phi (g _{2} ) \phi (g _{1} g _{2} ) ^{-1} = \mathop{\rm Int}\nolimits \ m (g _{1} ,\ g _{2} ), $$ $$ m (g _{1} ,\ g _{2} ) m (g _{1} g _{2} ,\ g _{3} ) = \phi (g _{1} ) (m (g _{2} ,\ g _{3} )) m (g _{1} ,\ g _{2} \ g _{3} ); $$ here $ \mathop{\rm Int}\nolimits \ a $ is the inner automorphism generated by the element $ a \in A $. Define an equivalence relation in $ {\mathcal Z} ^{2} (G,\ A) $ by putting $ (m,\ \phi ) \sim (m ^ \prime ,\ \phi ^ \prime ) $ if there is a mapping $ h: \ G \rightarrow A $ such that $$ \phi ^ \prime (g) = ( \mathop{\rm Int}\nolimits \ h (g)) \phi (g) $$ and $$ m ^ \prime (g _{1} ,\ g _{2} ) = h (g _{1} ) ( \phi (g _{1} ) (h (g _{2} ))) m (g _{1} ,\ g _{2} ) h (g _{1} ,\ g _{2} ) ^{-1} . $$ The equivalence classes thus obtained are the elements of the cohomology set $ {\mathcal H} ^{2} (G,\ A) $. They are in one-to-one correspondence with the equivalence classes of extensions of $ A $ by $ G $( see Extension of a group).
The correspondence $ (m,\ \phi ) \rightarrow \phi $ gives a mapping $ \theta $ of the set $ {\mathcal H} ^{2} (G,\ A) $ into the set of all homomorphisms $$ G \rightarrow \mathop{\rm Out}\nolimits \ A = \mathop{\rm Aut}\nolimits \ A/ \mathop{\rm Int}\nolimits \ A; $$ let $ H _ \alpha ^{2} (G,\ A) = \theta ^{-1} ( \alpha ) $ for $ \alpha \in \mathop{\rm Out}\nolimits \ A $. If one fixes $ \alpha \in \mathop{\rm Out}\nolimits \ A $, the centre $ Z (A) $ of $ A $ takes on the structure of a $ G $- module and so the cohomology groups $ H ^{k} (G,\ Z (A)) $ are defined. It turns out that $ H _ \alpha ^{2} (G,\ A) $ is non-empty if and only if a certain class in $ H ^{3} (G,\ Z (A)) $ is trivial. Moreover, under this condition the group $ H ^{2} (G,\ Z (A)) $ acts simplely transitively on the set $ H _ \alpha ^{2} (G,\ A) $.
This definition of a two-dimensional cohomology can be generalized, carrying it over to sites (see [2], where the applications of this concept are also presented). A general algebraic scheme that yields a two-dimensional cohomology is outlined in [4]; just as in the special case described above, computation of two-dimensional cohomology reduces to the computation of one-dimensional non-Abelian and ordinary Abelian cohomology.
References
| [1] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) MR0180551 Zbl 0128.26303 |
| [2] | J. Giraud, "Cohomologie non abélienne" , Springer (1971) MR0344253 Zbl 0226.14011 |
| [3] | A.L. Onishchik, "Some concepts and applications of the theory of non-Abelian cohomology" Trans. Moscow Math. Soc. , 17 (1979) pp. 49–98 Trudy Moskov. Mat. Obshch. , 17 (1967) pp. 45–88 |
| [4] | A.K. Tolpygo, "Two-dimensional cohomologies and the spectral sequence in the nonabelian theory" Selecta Math. Sov. , 6 (1987) pp. 177–197 MR0548342 Zbl 0619.18006 |
| [5] | P. Dedecker, "Three-dimensional nonabelian cohomology for groups" , Category theory, homology theory and their applications (Battelle Inst. Conf.) , 2 , Springer (1968) pp. 32–64 |
| [6] | J. Frenkel, "Cohomology non abélienne et espaces fibrés" Bull. Soc. Math. France , 85 : 2 (1957) pp. 135–220 |
| [7] | H. Goldschmidt, "The integrability problem for Lie equations" Bull. Amer. Math. Soc. , 84 : 4 (1978) pp. 531–546 MR0517116 Zbl 0439.58025 |
| [8] | T.A. Springer, "Nonabelian 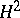 in Galois cohomology" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 164–182 MR209297 Zbl 0193.48902 in Galois cohomology" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 164–182 MR209297 Zbl 0193.48902 |
Non-Abelian cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-Abelian_cohomology&oldid=24152