Toeplitz C*-algebra
A uniformly closed  -algebra of operators on a Hilbert space (a uniformly closed
-algebra of operators on a Hilbert space (a uniformly closed  -algebra). Such algebras are closely connected to important fields of geometric analysis, e.g., index theory, geometric quantization and several complex variables.
-algebra). Such algebras are closely connected to important fields of geometric analysis, e.g., index theory, geometric quantization and several complex variables.
In the one-dimensional case one considers the Hardy space  over the one-dimensional torus
over the one-dimensional torus 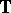 (cf. also Hardy spaces), and defines the Toeplitz operator
(cf. also Hardy spaces), and defines the Toeplitz operator  with "symbol" function
with "symbol" function  by
by 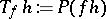 for all
for all 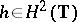 , where
, where 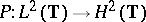 is the orthogonal projection given by the Cauchy integral theorem. The
is the orthogonal projection given by the Cauchy integral theorem. The 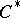 -algebra
-algebra  generated by all operators
generated by all operators 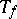 with continuous symbol
with continuous symbol  is not commutative, but defines a
is not commutative, but defines a 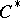 -algebra extension
-algebra extension
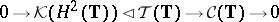 |
of the  -algebra
-algebra 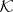 of all compact operators; in fact, this "Toeplitz extension" is the generator of the Abelian group
of all compact operators; in fact, this "Toeplitz extension" is the generator of the Abelian group 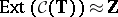 .
.
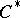 -algebra extensions are the building blocks of
-algebra extensions are the building blocks of  -theory and index theory; in our case a Toeplitz operator
-theory and index theory; in our case a Toeplitz operator 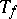 is Fredholm (cf. also Fredholm operator) if
is Fredholm (cf. also Fredholm operator) if 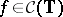 has no zeros, and then the index
has no zeros, and then the index 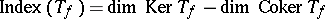 is the (negative) winding number of
is the (negative) winding number of 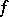 .
.
In the multi-variable case, Toeplitz  -algebras have been studied in several important cases, e.g. for strictly pseudo-convex domains
-algebras have been studied in several important cases, e.g. for strictly pseudo-convex domains 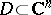 [a1], including the unit ball
[a1], including the unit ball 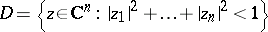 [a2], [a10], for tube domains and Siegel domains over convex "symmetric" cones [a5], [a8], and for general bounded symmetric domains in
[a2], [a10], for tube domains and Siegel domains over convex "symmetric" cones [a5], [a8], and for general bounded symmetric domains in 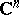 having a transitive semi-simple Lie group of holomorphic automorphisms [a7]. Here, the principal new feature is the fact that Toeplitz operators
having a transitive semi-simple Lie group of holomorphic automorphisms [a7]. Here, the principal new feature is the fact that Toeplitz operators 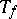 (say, on the Hardy space
(say, on the Hardy space 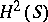 over the Shilov boundary
over the Shilov boundary 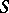 of a pseudo-convex domain
of a pseudo-convex domain 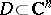 ) with continuous symbols
) with continuous symbols 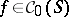 are not essentially commuting, i.e.
are not essentially commuting, i.e.
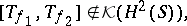 |
in general. Thus, the corresponding Toeplitz 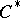 -algebra
-algebra 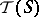 is not a (one-step) extension of
is not a (one-step) extension of  ; instead one obtains a multi-step
; instead one obtains a multi-step 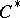 -filtration
-filtration
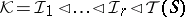 |
of 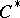 -ideals, with essentially commutative subquotients
-ideals, with essentially commutative subquotients 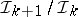 , whose maximal ideal space (its spectrum) reflects the boundary strata of the underlying domain. The length
, whose maximal ideal space (its spectrum) reflects the boundary strata of the underlying domain. The length  of the composition series is an important geometric invariant, called the rank of
of the composition series is an important geometric invariant, called the rank of 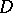 . The index theory and
. The index theory and 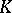 -theory of these multi-variable Toeplitz
-theory of these multi-variable Toeplitz 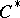 -algebras is more difficult to study; on the other hand one obtains interesting classes of operators arising by geometric quantization of the underlying domain
-algebras is more difficult to study; on the other hand one obtains interesting classes of operators arising by geometric quantization of the underlying domain 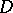 , regarded as a complex Kähler manifold.
, regarded as a complex Kähler manifold.
A general method for studying the structure and representations of Toeplitz 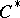 -algebras, at least for Shilov boundaries
-algebras, at least for Shilov boundaries 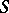 arising as a symmetric space (not necessarily Riemannian), is the so-called
arising as a symmetric space (not necessarily Riemannian), is the so-called 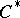 -duality [a11], [a9]. For example, if
-duality [a11], [a9]. For example, if  is a Lie group with (reduced) group
is a Lie group with (reduced) group 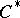 -algebra
-algebra  , then the so-called co-crossed product
, then the so-called co-crossed product 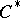 -algebra
-algebra  induced by a natural co-action
induced by a natural co-action 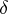 can be identified with
can be identified with 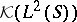 . Now the Cauchy–Szegö orthogonal projection
. Now the Cauchy–Szegö orthogonal projection 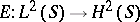 (cf. also Cauchy operator) defines a certain
(cf. also Cauchy operator) defines a certain 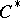 -completion
-completion 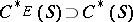 , and the corresponding Toeplitz
, and the corresponding Toeplitz 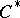 -algebra
-algebra  can be realized as (a corner of)
can be realized as (a corner of) 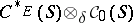 . In this way the well-developed representation theory of (co-) crossed product
. In this way the well-developed representation theory of (co-) crossed product  -algebras [a4] can be applied to obtain Toeplitz
-algebras [a4] can be applied to obtain Toeplitz 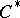 -representations related to the boundary
-representations related to the boundary 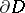 . For example, the two-dimensional torus
. For example, the two-dimensional torus 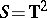 gives rise to non-type-
gives rise to non-type-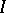
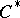 -algebras (for cones with irrational slopes), and the underlying "Reinhardt" domains (cf. also Reinhardt domain) have interesting complex-analytic properties, such as a non-compact solution operator of the Neumann
-algebras (for cones with irrational slopes), and the underlying "Reinhardt" domains (cf. also Reinhardt domain) have interesting complex-analytic properties, such as a non-compact solution operator of the Neumann 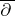 -problem [a6].
-problem [a6].
References
| [a1] | L. Boutet de Monvel, "On the index of Toeplitz operators of several complex variables" Invent. Math. , 50 (1979) pp. 249–272 Zbl 0398.47018 |
| [a2] | L. Coburn, "Singular integral operators and Toeplitz operators on odd spheres" Indiana Univ. Math. J. , 23 (1973) pp. 433–439 MR0322595 Zbl 0271.46052 |
| [a3] | R. Douglas, R. Howe, "On the 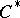 -algebra of Toeplitz operators on the quarter-plane" Trans. Amer. Math. Soc. , 158 (1971) pp. 203–217 MR288591 -algebra of Toeplitz operators on the quarter-plane" Trans. Amer. Math. Soc. , 158 (1971) pp. 203–217 MR288591 |
| [a4] | M. Landstad, J. Phillips, I. Raeburn, C. Sutherland, "Representations of crossed products by coactions and principal bundles" Trans. Amer. Math. Soc. , 299 (1987) pp. 747–784 MR0869232 Zbl 0722.46031 |
| [a5] | P. Muhly, J. Renault, "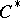 -algebras of multivariable Wiener–Hopf operators" Trans. Amer. Math. Soc. , 274 (1982) pp. 1–44 MR0670916 Zbl 0509.46050 Zbl 0509.46049 -algebras of multivariable Wiener–Hopf operators" Trans. Amer. Math. Soc. , 274 (1982) pp. 1–44 MR0670916 Zbl 0509.46050 Zbl 0509.46049 |
| [a6] | N. Salinas, A. Sheu, H. Upmeier, "Toeplitz operators on pseudoconvex domains and foliation algebras" Ann. Math. , 130 (1989) pp. 531–565 MR1025166 Zbl 0708.47021 |
| [a7] | H. Upmeier, "Toeplitz 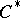 -algebras on bounded symmetric domains" Ann. Math. , 119 (1984) pp. 549–576 MR744863 -algebras on bounded symmetric domains" Ann. Math. , 119 (1984) pp. 549–576 MR744863 |
| [a8] | H. Upmeier, "Toeplitz operators on symmetric Siegel domains" Math. Ann. , 271 (1985) pp. 401–414 MR0787189 Zbl 0565.47016 |
| [a9] | H. Upmeier, "Toeplitz operators and index theory in several complex variables" , Birkhäuser (1996) MR1384981 Zbl 0957.47023 |
| [a10] | U. Venugopalkrishna, "Fredholm operators associated with strongly pseudoconvex domains in 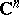 " J. Funct. Anal. , 9 (1972) pp. 349–373 MR0315502 Zbl 0241.47023 " J. Funct. Anal. , 9 (1972) pp. 349–373 MR0315502 Zbl 0241.47023 |
| [a11] | A. Wassermann, "Algèbres d'opérateurs de Toeplitz sur les groupes unitaires" C.R. Acad. Sci. Paris , 299 (1984) pp. 871–874 MR0777751 |
Toeplitz C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Toeplitz_C*-algebra&oldid=24133