Masser-Philippon/Lazard-Mora example
Lazard–Mora/Masser–Philippon example, Lazard–Mora example, Masser–Philippon example
An extremal family for the degrees in the Hilbert Nullstellensatz (cf. Hilbert theorem) is given by the following example, ascribed variously to D.W. Masser and P. Philippon and to D. Lazard and T. Mora:
\begin{equation*} f _ { 1 } : = x _ { 1 } ^ { d }, \end{equation*}
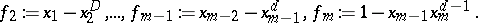 |
The $f_i$ are readily seen to have no common zeros. If $a _ { 1 } , \dots , a _ { m }$ are polynomials such that
\begin{equation*} a _ { 1 } f _ { 1 } + \ldots + a _ { m } f _ { m } = 1, \end{equation*}
by evaluation on the rational curve
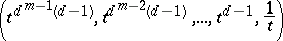 |
it is easy to see that $\operatorname{deg}_{x_m} a _ { 1 } \geq d ^ { m - 1 } ( d - 1 )$. This lower bound of order $d ^ { m }$ for the degrees of the coefficients for the Nullstellensatz is much better than the doubly exponential lower bound for the general ideal membership problem given in [a2]. Variants of the example, cf. [a3], show that the terms in the Liouville–Łojasiewicz inequality are nearly optimal, with the presumed exception depending solely on the degree.
Another family of extremal examples for the Nullstellensatz is given in [a1].
References
| [a1] | J. Kollár, "Sharp effective Nullstellensatz" J. Amer. Math. Soc. , 1 (1988) pp. 963–975 |
| [a2] | E.W. Mayr, A.R. Meyer, "The complexity of the word problems in commutative semigroups and polynlomial ideals" Adv. Math. , 46 (1982) pp. 305–329 |
| [a3] | W.D. Brownawell, "Local diophantine Nullstellen equalities" J. Amer. Math. Soc. , 1 (1988) pp. 311–322 |
Masser-Philippon/Lazard-Mora example. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Masser-Philippon/Lazard-Mora_example&oldid=22793