Bishop-Phelps theorem
Consider a real Banach space  , its (closed convex) unit ball
, its (closed convex) unit ball  , and its adjoint space of continuous linear functionals
, and its adjoint space of continuous linear functionals  (cf. Linear functional). If
(cf. Linear functional). If  , its norm is defined as its supremum on the closed convex set
, its norm is defined as its supremum on the closed convex set  , that is,
, that is,  . The fundamental Hahn–Banach theorem implies that if
. The fundamental Hahn–Banach theorem implies that if 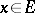 and
and  , then there exists a continuous linear functional
, then there exists a continuous linear functional  such that
such that 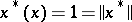 . Thus, these "Hahn–Banach functionals" attain their suprema on
. Thus, these "Hahn–Banach functionals" attain their suprema on  , and by taking all positive scalar multiples of such functions, there are clearly "many" of them. The Bishop–Phelps theorem [a1] asserts that such norm-attaining functionals are actually norm dense in
, and by taking all positive scalar multiples of such functions, there are clearly "many" of them. The Bishop–Phelps theorem [a1] asserts that such norm-attaining functionals are actually norm dense in 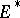 . (James' theorem [a4] shows that if every element of
. (James' theorem [a4] shows that if every element of 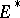 attains its supremum on
attains its supremum on 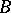 , then
, then 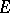 is necessarily reflexive, cf. Reflexive space.) A more general Bishop–Phelps theorem yields the same norm density conclusion for the set of functionals in
is necessarily reflexive, cf. Reflexive space.) A more general Bishop–Phelps theorem yields the same norm density conclusion for the set of functionals in 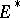 which attain their supremum on an arbitrary non-empty closed convex bounded subset
which attain their supremum on an arbitrary non-empty closed convex bounded subset 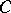 of
of 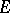 (the support functionals of
(the support functionals of 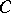 ). In fact, if
). In fact, if 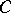 is any non-empty closed convex subset of
is any non-empty closed convex subset of 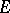 , its support functionals are norm dense among those functionals which are bounded above on
, its support functionals are norm dense among those functionals which are bounded above on 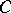 ; moreover, the points of
; moreover, the points of 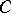 at which support functionals attain their supremum on
at which support functionals attain their supremum on 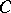 (the support points) are dense in the boundary of
(the support points) are dense in the boundary of 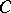 . (This contrasts with a geometric version of the Hahn–Banach theorem, which guarantees that every boundary point of a closed convex set
. (This contrasts with a geometric version of the Hahn–Banach theorem, which guarantees that every boundary point of a closed convex set 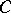 is a support point, provided
is a support point, provided 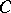 has non-empty interior.)
has non-empty interior.)
This last result leads to the Brøndsted–Rockafellar theorem [a2], fundamental in convex analysis, about extended-real-valued lower semi-continuous convex functions 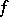 on
on 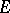 which are proper, in the sense that
which are proper, in the sense that 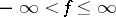 and
and 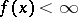 for at least one point
for at least one point  . The epigraph
. The epigraph 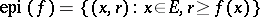 of such a function is a non-empty closed convex subset of the product space
of such a function is a non-empty closed convex subset of the product space 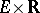 (
(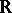 the real numbers) and the subgradients of
the real numbers) and the subgradients of  define support functionals of
define support functionals of 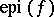 . The set of all subgradients to
. The set of all subgradients to 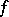 at
at  (where
(where 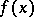 is finite) form the subdifferential
is finite) form the subdifferential
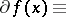 |
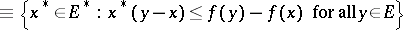 |
of 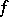 at
at  . The Brøndsted–Rockafellar theorem [a2] yields density, within the set of points where
. The Brøndsted–Rockafellar theorem [a2] yields density, within the set of points where 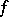 is finite, of those
is finite, of those  for which
for which  is non-empty.
is non-empty.
See also [a3] for the Bishop–Phelps and James theorems, [a5] for the Bishop–Phelps and Brøndsted–Rockafellar theorems.
References
| [a1] | E. Bishop, R.R. Phelps, "The support functionals of a convex set" P. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 27–35 Zbl 0149.08601 |
| [a2] | A. Brøndsted, R.T. Rockafellar, "On the subdifferentiability of convex functions" Proc. Amer. Math. Soc. , 16 (1965) pp. 605–611 |
| [a3] | J. Diestel, "Geometry of Banach spaces: Selected topics" , Lecture Notes in Mathematics , 485 , Springer (1975) |
| [a4] | R.C. James, "Reflexivity and the supremum of linear functionals" Israel J. Math. , 13 (1972) pp. 289–300 |
| [a5] | R.R. Phelps, "Convex functions, monotone operators and differentiability" , Lecture Notes in Mathematics , 1364 , Springer (1993) (Edition: Second) |
| [b1] | Andrzej Granas, James Dugundji, "Fixed Point Theory", Springer Monographs in Mathematics, Springer (2003) ISBN 0-387-00173-5 Zbl 1025.47002 |
Bishop-Phelps theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bishop-Phelps_theorem&oldid=22129