Markov property
for a real-valued stochastic process 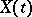 ,
, 
2020 Mathematics Subject Classification: Primary: 60Jxx [MSN][ZBL]
The property that for any set 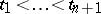 of times from
of times from  and any Borel set
and any Borel set 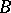 ,
,
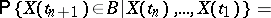 | (*) |
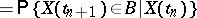 |
with probability 1, that is, the conditional probability distribution of 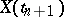 given
given 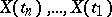 coincides (almost certainly) with the conditional distribution of
coincides (almost certainly) with the conditional distribution of 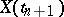 given
given 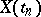 . This can be interpreted as independence of the "future"
. This can be interpreted as independence of the "future" 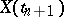 and the "past"
and the "past" 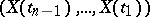 given the fixed "present"
given the fixed "present"  . Stochastic processes satisfying the property (*) are called Markov processes (cf. Markov process). The Markov property has (under certain additional assumptions) a stronger version, known as the "strong Markov property" . In discrete time
. Stochastic processes satisfying the property (*) are called Markov processes (cf. Markov process). The Markov property has (under certain additional assumptions) a stronger version, known as the "strong Markov property" . In discrete time 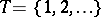 the strong Markov property, which is always true for (Markov) sequences satisfying (*), means that for each stopping time
the strong Markov property, which is always true for (Markov) sequences satisfying (*), means that for each stopping time  (relative to the family of
(relative to the family of 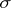 -algebras
-algebras 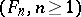 ,
, 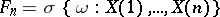 ), with probability one
), with probability one
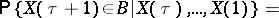 |
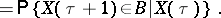 |
References
| [1] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) MR0375463 Zbl 0305.60027 |
Comments
References
| [a1] | K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1960) MR0116388 Zbl 0092.34304 |
| [a2] | J.L. Doob, "Stochastic processes" , Wiley (1953) MR1570654 MR0058896 Zbl 0053.26802 |
| [a3] | E.B. Dynkin, "Markov processes" , 1 , Springer (1965) (Translated from Russian) MR0193671 Zbl 0132.37901 |
| [a4] | T.G. Kurtz, "Markov processes" , Wiley (1986) MR0838085 Zbl 0592.60049 |
| [a5] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1966) MR0210154 Zbl 0138.10207 |
| [a6] | P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965) MR0190953 Zbl 0137.11602 |
| [a7] | M. Loève, "Probability theory" , II , Springer (1978) MR0651017 MR0651018 Zbl 0385.60001 |
Markov property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_property&oldid=21658