Bateman-Horn conjecture
A conjecture on the asymptotic behaviour of a polynomial satisfying the Bunyakovskii condition (cf. also Bunyakovskii conjecture).
Let 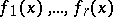 be polynomials (cf. Polynomial) with integer coefficients, of degrees
be polynomials (cf. Polynomial) with integer coefficients, of degrees 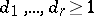 , irreducible (cf. Irreducible polynomial), and with positive leading coefficients. Let
, irreducible (cf. Irreducible polynomial), and with positive leading coefficients. Let
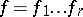 |
be their product.
V. Bunyakovskii considered the case 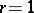 and asked whether
and asked whether 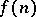 could represent infinitely many prime numbers as
could represent infinitely many prime numbers as  ranges over the positive integers. An obvious necessary condition is that all coefficients of
ranges over the positive integers. An obvious necessary condition is that all coefficients of  be relatively prime. However, that is not sufficient. He conjectured that, in addition, the following Bunyakovskii condition is sufficient: there is no prime number
be relatively prime. However, that is not sufficient. He conjectured that, in addition, the following Bunyakovskii condition is sufficient: there is no prime number 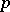 dividing all the values
dividing all the values 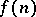 for the positive integers
for the positive integers  (cf. Bunyakovskii conjecture).
(cf. Bunyakovskii conjecture).
Assuming the Bunyakovskii condition, let
 |
where  is the number of solutions of the congruence equation
is the number of solutions of the congruence equation 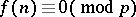 (for
(for 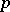 prime). The Bateman–Horn conjecture asserts that
prime). The Bateman–Horn conjecture asserts that
 |
where 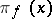 is the number of positive integers
is the number of positive integers  such that all
such that all 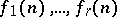 are prime.
are prime.
This formula gives the density of primes in an arithmetic progression (cf. Dirichlet theorem), using the polynomial 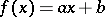 . After some computations, it gives the asymptotic behaviour conjectured by G.H. Hardy and J.E. Littlewood for the number of primes representable by the polynomial
. After some computations, it gives the asymptotic behaviour conjectured by G.H. Hardy and J.E. Littlewood for the number of primes representable by the polynomial  . It also gives the Hardy–Littlewood conjecture for the behaviour of the number of twin primes, by applying the formula to the polynomials
. It also gives the Hardy–Littlewood conjecture for the behaviour of the number of twin primes, by applying the formula to the polynomials  and
and  (cf. also Twins). Similarly, it implies many other conjectures of Hardy and Littlewood stated in [a2].
(cf. also Twins). Similarly, it implies many other conjectures of Hardy and Littlewood stated in [a2].
See also Distribution of prime numbers.
References
| [a1] | P.T. Bateman, R. Horn, "A heuristic formula concerning the distribution of prime numbers" Math. Comp. , 16 (1962) pp. 363–367 |
| [a2] | G.H. Hardy, J.E. Littlewood, "Some problems of Partitio Numerorum III" Acta Math. , 44 (1922) pp. 1–70 |
| [a3] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
Bateman-Horn conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bateman-Horn_conjecture&oldid=19202