Markov chain, decomposable

2020 Mathematics Subject Classification: Primary: 60J10 Secondary: 60J27 [MSN][ZBL]

A Markov chain whose transition probabilities 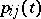have the following property: There are states 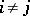such that 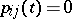for all 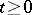. Decomposability of a Markov chain is equivalent to decomposability of its matrix of transition probabilities 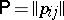for discrete-time Markov chains, and of its matrix of transition probability densities 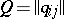, , 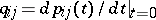for continuous-time Markov chains. The state space of a decomposable Markov chain consists either of inessential states or of more than one class of communicating states (cf. Markov chain).

References

[a1]	W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1966)
[a2]	D. Freedman, "Markov chains" , Holden-Day (1975)
[a3]	M. Iosifescu, "Finite Markov processes and their applications" , Wiley (1980)
[a4]	J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960)
[a5]	J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains" , Springer (1976)
[a6]	D. Revuz, "Markov chains" , North-Holland (1975)
[a7]	V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian)
[a8]	E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981)