Darboux property

A function $f : \mathbf{R} \rightarrow \mathbf{R}$ (where $\mathbf{R}$ denotes the set of all real numbers with the natural metric; cf. also Real number) is said to have the intermediate value property if, whenever $x$, $y$ are real numbers and is any number between $f ( x )$ and $f ( y )$, there exists a number $t$ between $x$ and $y$ such that $f ( t ) = \epsilon$. In the 19th century some mathematicians believed that this property is equivalent to continuity. In 1875, G. Darboux [a7] showed that every finite derivative has the intermediate value property and he gave an example of discontinuous derivatives. The intermediate value property is usually called the Darboux property, and a Darboux function is a function having this property. For an arbitrary function $g : \mathbf{R} \rightarrow \mathbf{R}$ there exists a Darboux function $f$ such that $f ( x ) = g ( x )$ everywhere except on a set of the first category (cf. also Baire classes) and of Lebesgue measure zero. If $g$ is a measurable function (respectively, belongs to a Baire class $\alpha$), then $f$ can be chosen to be measurable (respectively, to belong to Baire class $\alpha$).

In [a2], the notion of a "Darboux point" was introduced, leading to a local characterization of the Darboux property (see also [a16]). Let $C _ { f }$ (respectively, 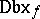) be the set of all continuity (respectively, Darboux) points of $f$. Then ([a3]) $f : \mathbf{R} \rightarrow \mathbf{R}$ is a Darboux function if and only if $\mathbf{R} = \text{Dbx} _ { f }$. One can prove ([a21]) that 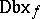is a $G _ { \delta }$-set (cf. also Set of type $F _ { \sigma }$ ($G _ { \delta }$)) and, of course, $C _ { f } \subset \operatorname {Dbx} _ { f }$. Conversely [a4], [a16], if $C \subset D$ are $G _ { \delta }$-sets, then there exists a function $f$ such that $C = C _ { f }$ and $D = \operatorname{Dbx} _ { f }$.

Every continuous function and every approximately continuous function (cf. Approximate continuity) has the Darboux property [a6] and this is also true for a finite (approximate) derivative, [a13], [a10]. In the case of an infinite derivative, the following result holds ([a26], [a14]): If $f$ is Darboux (respectively, approximately continuous) and $f ^ { \prime }$ (respectively, $f _ { \operatorname{ap} } ^ { \prime }$) exists everywhere (finite or infinite), then $f ^ { \prime }$ (respectively, $f _ { \operatorname{ap} } ^ { \prime }$) is a Darboux function.

The simplest example of a Darboux discontinuous function is the function

\begin{equation*} f ( x ) = \left\{ \begin{array} { l l } { \operatorname { sin } \frac { 1 } { x } , } & { x \neq 0, } \\ { a , } & { x = 0, } \end{array} \right. \end{equation*}

where $a \in [ - 1,1 ]$ (if $a = 0$, $f$ is a derivative, and if $a \neq 0$ $f$ is not a derivative). There exist Darboux functions that are discontinuous at each point of their domain (e.g. [a2]).

In spite of the fact that the Darboux property is close to continuity, the class of Darboux functions has some peculiar properties. For example, the class of all Darboux functions is not closed with respect to the fundamental operations of addition, multiplication, uniform convergence, etc. In particular, every function $f$ is the sum of two Darboux functions. In 1959, H. Fast proved [a8] that for every family $\mathcal{F}$ of functions that has the cardinality of the continuum there is a Darboux function $g$ such that the sum of $g$ and any function from $\mathcal{F}$ has the Darboux property. Conversely (under the continuum hypothesis or the Martin axiom, cf. also Suslin hypothesis), there exists a Darboux function $h$ such that $f + h$ is not Darboux, for every continuous, nowhere constant function $f$ (thus, $h$ is "universally bad" ; [a15]). However, under quite natural assumptions (see, e.g., [a22], [a23]) on a Darboux function $f$ whose set of all discontinuity points is nowhere dense (this function can be Lebesgue non-measurable), there exists a ring $R ( f )$ of Darboux functions, containing the class of all continuous functions, such that $f \in R ( f )$. The existence of such an algebraic structure for Darboux functions is connected with the existence of some special topologies on the real line.

Generalizations.

The main generalizations of the notion of a Darboux function are connected with the consideration of functions mapping a topological space into a topological space, and with the observation that a real function of a real variable has the Darboux property if and only if the image of any interval is a connected set (the Darboux property can be characterized in terms of images but not in terms of pre-images). The main idea of these generalizations can be described as follows: For a family $\mathcal Z$ of sets (for example, all connected sets, all arcs, etc.), one says that a function $f$ is a Darboux function if $f ( E )$ is a connected set for each $E \in \mathcal{Z}$ (see, e.g., [a9], [a25], [a19], [a12], [a18], [a1]). Thus, for example, it is possible to consider relationships between the existence of rings of Darboux functions and Darboux homotopies (see, e.g., [a24]), as well as problems connected with the monotonicity of Darboux functions defined on a topological space (see, e.g., [a9]) and Darboux retracts (see, e.g., [a20]).

Let $f : X \rightarrow Y$, where $X$, $Y$ are topological spaces. Consider the following families of functions:

$D$: the family of Darboux functions;

$\operatorname { Conn}$: the class of all connectivity functions;

$\operatorname{ACS}$: the class of all almost-continuous functions in the sense of Stallings;

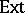: the family of all extendable functions. In the literature, functions from these classes are called Darboux-like functions, [a11]. In the class of functions mapping the real line into the real line the following (proper) inclusions hold:

\begin{equation*} C \subset \operatorname{Ext} \subset \operatorname{ACS} \subset\operatorname{Conn} \subset D, \end{equation*}

(where $C$ is the family of all continuous functions). The investigations connected with the properties of Darboux-like functions concentrate around the characterizations of these families, relationships between these classes, algebraic operations, and considerations connected with cardinal functions (see, e.g., [a11], [a17]).

The Darboux property has also been considered for multi-valued functions (see, e.g., [a5]).

References

[a1]	A.M. Bruckner, J.B. Bruckner, "Darboux transformations" Trans. Amer. Math. Soc. , 128 (1967) pp. 103–111
[a2]	A.M. Bruckner, J.C. Ceder, "Darboux continuity" Jahresber. Deutsch. Math. Ver. , 67 (1965) pp. 93–117
[a3]	A. Császár, "Sur la propriété de Darboux" C.R. Prem. Congres des Math. Hongor. Budapest (1952) pp. 551–560
[a4]	J. Ceder, "On factoring a function into a product of Darboux functions" Rend. Circ. Mat. Palermo , 31 (1982) pp. 16–22
[a5]	J. Ceder, "Characterizations of Darboux selections" Rend. Circ. Mat. Palermo , 30 (1981) pp. 461–470
[a6]	A. Denjoy, "Sur les fonctions dérivées sommables" Soc. Math. France , 43 (1915) pp. 161–248
[a7]	G. Darboux, "Memoire sur les fonctions discontinuea" Ann. Sci. Scuola Norm. Sup. , 4 (1875) pp. 161–248
[a8]	H. Fast, "Une remarque sur la properiété de Weierstrass" Colloq. Math. , 7 (1959) pp. 75–77
[a9]	K.M. Garg, "Properties of connected functions in terms of their levels" Fund. Math. , 47 (1977) pp. 17–36
[a10]	C. Goffman, C. Neugebauer, "An approximate derivatives" Proc. Amer. Math. Soc. , 11 (1960) pp. 962–966
[a11]	R.G. Gibson, T. Natkaniec, "Darboux like functions" Real Anal. Exch. , 22 : 2 (1996/97) pp. 492–533
[a12]	R. Hrycay, "Weakly connected functions" PhD Thesis Univ. Alberta (1971)
[a13]	A. Khintchine, "Recherehes sur la structure des fonctions measurables" Fund. Math. , 9 (1927) pp. 217–279
[a14]	M. Kulbacka, "Sur certaines properiétés des dérivées approximatives" Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys. , 12 : 1 (1964) pp. 17–20
[a15]	B. Kirchheim, T. Natkaniec, "On universally bad Darboux functions" Real Anal. Exch. , 16 (1990/91) pp. 481–486
[a16]	J.L. Lipiński, "On Darboux points" Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys. , 26 : 11 (1978) pp. 869–873
[a17]	A. Maliszewski, "Darboux property and quasi-continuity. A uniform approach" Habilitation Thesis Słupsk (1996)
[a18]	C.J. Neugebauer, "Darboux property for functions of several variables" Trans. Amer. Math. Soc. , 107 (1963) pp. 30–37
[a19]	W. Pervin, N. Levine, "Connected mappings of Hausdorff spaces" Proc. Amer. Math. Soc. , 9 (1958) pp. 488–495
[a20]	F. Roush, R. Gibson, K. Kellum, "Darboux retracts" Proc. Amer. Math. Soc. , 60 (1976) pp. 183–184
[a21]	H. Rosen, "Connectivity points and Darboux points of a real functions" Fund. Math. , 89 (1975) pp. 265–269
[a22]	R.J. Pawlak, "On rings of Darboux functions" Colloq. Math. , 53 (1987) pp. 283–300
[a23]	H. Pawlak, R.J. Pawlak, "Fundamental rings for classes of Darboux functions" Real Anal. Exch. , 14 (1988/89) pp. 189–202
[a24]	R.J. Pawlak, "Darboux homotopies and Darboux retracts - results and questions" Real Anal. Exch. , 20 : 2 (1994/95) pp. 805–814
[a25]	R.J. Pawlak, "Darboux transformations" Habilitation Thesis Univ. Lodz (1985) (In Polish)
[a26]	Z. Zahorski, "Sur la classe de Baire des dérivées approximatives d'una fonction quelconque" Ann. Soc. Polon. Math. , 21 (1948) pp. 306–323