Bürmann-Lagrange series
Lagrange series
A power series which offers a complete solution to the problem of local inversion of holomorphic functions. In fact, let a function 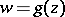 of the complex variable
of the complex variable  be regular in a neighbourhood of the point
be regular in a neighbourhood of the point  , and let
, and let 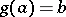 and
and 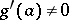 . Then there exists a regular function
. Then there exists a regular function 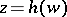 in some neighbourhood of the point
in some neighbourhood of the point 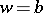 of the
of the 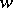 -plane which is the inverse to
-plane which is the inverse to 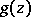 and is such that
and is such that 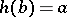 . Moreover, if
. Moreover, if  is any regular function in a neighbourhood of the point
is any regular function in a neighbourhood of the point  , then the composite function
, then the composite function  can be expanded in a Bürmann–Lagrange series in a neighbourhood of the point
can be expanded in a Bürmann–Lagrange series in a neighbourhood of the point 
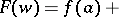 | (*) |
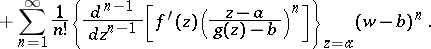 |
The inverse of the function 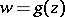 is obtained by setting
is obtained by setting 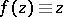 .
.
The expansion (*) follows from Bürmann's theorem [1]: Under the assumptions made above on the holomorphic functions 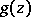 and
and 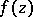 , the latter function may be represented in a certain domain in the
, the latter function may be represented in a certain domain in the  -plane containing
-plane containing  in the form
in the form
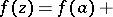 |
 |
where
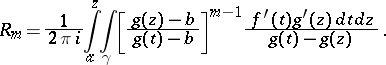 |
Here 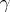 is a contour in the
is a contour in the 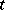 -plane which encloses the points
-plane which encloses the points  and
and  , and is such that if
, and is such that if 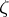 is any point inside
is any point inside 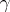 , then the equation
, then the equation 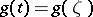 has no roots on
has no roots on 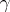 or inside
or inside 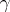 other than the simple root
other than the simple root 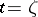 .
.
The expansion (*) for the case  was obtained by J.L. Lagrange .
was obtained by J.L. Lagrange .
If the derivative 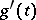 has a zero of order
has a zero of order 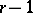 at the point
at the point  , there is the following generalization of the Bürmann–Lagrange series for the multi-valued inverse function [3]:
, there is the following generalization of the Bürmann–Lagrange series for the multi-valued inverse function [3]:
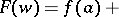 |
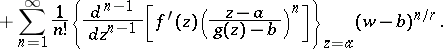 |
Another generalization (see, for example, [4]) refers to functions 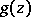 regular in an annulus; instead of the series (*), one obtains a series with positive and negative powers of the difference
regular in an annulus; instead of the series (*), one obtains a series with positive and negative powers of the difference 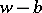 .
.
References
| [1] | H. Bürmann, Mem. Inst. Nat. Sci. Arts. Sci. Math. Phys. , 2 (1799) pp. 13–17 |
| [2a] | J.L. Lagrange, Mem. Acad. R. Sci. et Belles-lettres Berlin , 24 (1770) |
| [2b] | J.L. Lagrange, "Additions au mémoire sur la résolution des équations numériques" , Oeuvres , 2 , G. Olms (1973) pp. 579–652 |
| [3] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1968) pp. Chapt. 7 |
| [4] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
| [5] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
Comments
There is an exhaustive treatment of the Lagrange–Bürmann theorem and series in [a1].
References
| [a1] | P. Henrici, "Applied and computational complex analysis" , 1 , Wiley (1974) |
Bürmann-Lagrange series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=B%C3%BCrmann-Lagrange_series&oldid=18332