Markov inequality

for derivatives of algebraic polynomials

An equality giving an estimate of the uniform norm of the derivative in terms of the uniform norm of the polynomial itself. Let 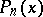be an algebraic polynomial of degree not exceeding and let

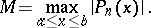Then for any in ,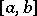

(*)

Inequality (*) was obtained by A.A. Markov in 1889 (see [1]). The Markov inequality is exact (best possible). Thus, for 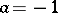, , 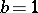considering the Chebyshev polynomials

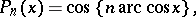then

and inequality (*) becomes an equality.

For derivatives of arbitrary order 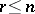, Markov's inequality implies that

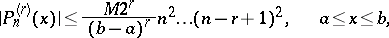which already for 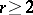is not exact. An exact inequality for was obtained by V.A. Markov [2]:

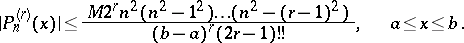References

[1]	A.A. Markov, "Selected works" , Moscow-Leningrad (1948) (In Russian)
[2]	W.A. [V.A. Markov] Markoff, "Ueber die Funktionen, die in einem gegebenen Intervall möglichst wenig von Null abweichen" Math. Ann. , 77 (1916) pp. 213–258
[3]	I.P. Natanson, "Constructive theory of functions" , 1–2 , F. Ungar (1964–1965) (Translated from Russian)

References

[a1]	E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982)
[a2]	R.J. Duffin, A.C. Schaeffer, "A refinement of an inequality of the brothers Markoff" Trans. Amer. Math. Soc. , 50 (1941) pp. 517–528
[a3]	A. Schönhage, "Approximationstheorie" , de Gruyter (1971)