Picard group

A group of classes of invertible sheaves (or line bundles). More precisely, let 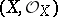be a ringed space. A sheaf of 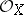-modules 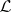is called invertible if it is locally isomorphic to the structure sheaf 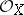. The set of classes of isomorphic invertible sheaves on 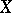is denoted by 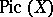. The tensor product 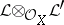defines an operation on the set 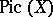, making it an Abelian group called the Picard group of 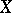. The group 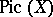is naturally isomorphic to the cohomology group 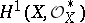, where is the sheaf of invertible elements in .

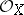For a commutative ring 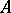, the Picard group 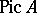is the group of classes of invertible 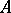-modules; 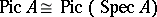. For a Krull ring, the group 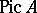is closely related to the divisor class group for this ring.

The Picard group of a complete normal algebraic variety 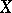has a natural algebraic structure (see Picard scheme). The reduced connected component of the zero of 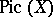is denoted by and is called the Picard variety for ; it is an algebraic group (an Abelian variety if 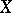is a complete non-singular variety). The quotient group 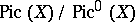is called the Néron–Severi group and it has a finite number of generators; its rank is called the Picard number. In the complex case, where 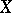is a smooth projective variety over 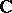, the group 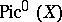is isomorphic to the quotient group of the space 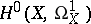of holomorphic 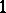-forms on 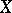by the lattice .

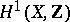References

[1]	D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701

References

[a1]	R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 MR0463157 Zbl 0367.14001