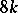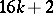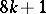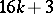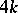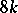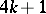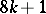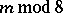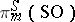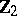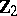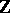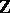Whitehead homomorphism
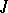-homomorphism
A homomorphism from the stable homotopy group of the spectrum of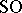 
to the stable homotopy group of the spectrum of the sphere 
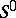, defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping 
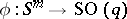determines a mapping 
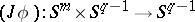, which can be extended to a mapping 
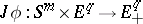of 
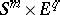to the upper hemi-sphere of 
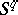. There is also an extension 
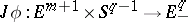to the lower hemi-sphere of 
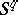, and this determines a mapping 
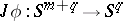. This construction gives a mapping of homotopy classes, and so defines a homomorphism 
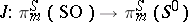, called the Whitehead group.
This homomorphism was first constructed by G.W. Whitehead , who also proved a theorem on the non-triviality of the infinite series of homotopy groups of spheres,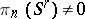 
, for the following values of 
and 
:'
<tbody> </tbody>
|
The stable homotopy groups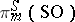 
are described by the Bott periodicity theorem [2]:'
<tbody> </tbody>
|
The image of the Whitehead homomorphism has been completely calculated (cf. [4], [5]): for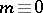 
(
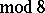) and 
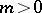the Whitehead group is a monomorphism and its image is a direct summand in the group 
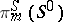; for 
(
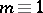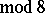) and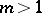 
the Whitehead group is a monomorphism on a direct summand of 
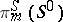; for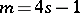 
the image of the Whitehead group is the cyclic group of order 
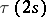, giving a direct summand in 
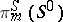, where 
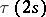is the denominator of the irreducible fraction 
, 
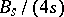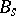being the 
-th Bernoulli number (cf. Bernoulli numbers).
References
| [1a] | G.W. Whitehead, "On the homotopy groups of spheres and rotation groups" Ann. of Math. , 43 (1942) pp. 634–640 MR0007107 Zbl 0060.41105 |
| [1b] | G.W. Whitehead, "A generalization of the Hopf invariant" Ann. of Math. , 51 (1950) pp. 192–237 MR0041435 Zbl 0045.44202 Zbl 0041.51903 |
| [2] | R. Bott, "The stable homotopy of the classical groups" Ann. of Math. , 70 (1959) pp. 313–337 MR0110104 Zbl 0129.15601 |
| [3a] | J.F. Adams, "On the groups 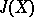 - I" Topology , 2 (1963) pp. 181–195 |
| [3b] | J.F. Adams, "On the groups 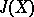 - II" Topology , 3 (1965) pp. 137–171 |
| [3c] | J.F. Adams, "On the groups 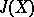 - III" Topology , 3 (1965) pp. 193–222 |
| [3d] | J.F. Adams, "On the groups 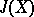 - IV" Topology , 5 (1966) pp. 21–71 |
| [4] | J.C. Becker, D.H. Gottlieb, "The transfer map and fiber bundles" Topology , 14 (1975) pp. 1–12 MR0377873 Zbl 0306.55017 |
| [5] | J.F. Adams, "Infinite loop spaces" , Princeton Univ. Press (1978) MR0505692 Zbl 0398.55008 |
Comments
Given a mapping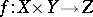 
of topological spaces, quite generally the Hopf construction gives a mapping
 |
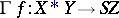from the join 
of 
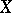and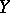 
to the suspension 
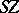of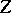 
, as follows. Consider
 |
The join 
is a certain quotient space of 
and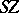 
is a quotient space of 
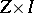. An elementary check shows that 
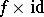is compatible with the corresponding equivalence relations, and hence defines a mapping 
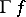as desired. Recall that 
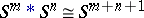, cf. Join.
Now, let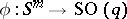 
be a mapping; each element of 
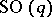induces a mapping 
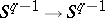of the 
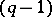-sphere into itself. Hence 
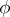induces a mapping
 |
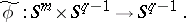Applying the Hopf construction to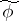 
gives the mapping 
:
 |
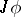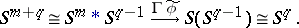References
| [a1] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 334 MR0402714 Zbl 0322.55001 |
| [a2] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. 480ff MR0385836 Zbl 0305.55001 |
Whitehead homomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_homomorphism&oldid=17616