Heinz-Kato-Furuta inequality
In the sequel, a capital letter denotes a bounded linear operator on a Hilbert space 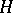 . An operator
. An operator 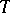 is said to be positive (denoted by
is said to be positive (denoted by 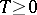 ) if
) if 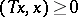 for all
for all 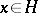 .
.
The following Heinz–Kato–Furuta inequality can be considered as an extension of the Heinz–Kato inequality, since for  the Heinz–Kato inequality is obtained from the Heinz–Kato–Furuta inequality.
the Heinz–Kato inequality is obtained from the Heinz–Kato–Furuta inequality.
The Heinz–Kato–Furuta inequality (1994; cf. [a2]): If 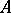 and
and 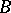 are positive operators such that
are positive operators such that 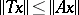 and
and 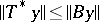 for all
for all 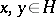 , then for all
, then for all 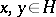 :
:
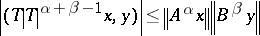 | (a1) |
for all 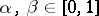 such that
such that 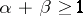 .
.
As generalizations of the Heinz–Kato–Furuta inequality, two determinant-type generalizations, expressed in terms of 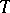 ,
, 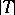 and
and 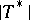 , can be obtained by using the Furuta inequality. It turns out that each of these two generalizations is equivalent to the Furuta inequality. Results similar to these determinant-type generalizations but under the conditions
, can be obtained by using the Furuta inequality. It turns out that each of these two generalizations is equivalent to the Furuta inequality. Results similar to these determinant-type generalizations but under the conditions 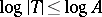 and
and 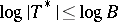 , which are weaker than the original conditions
, which are weaker than the original conditions 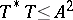 and
and 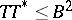 in the Heinz–Kato inequality, have also been obtained. A nice application of the Heinz–Kato–Furuta inequality is given in [a1].
in the Heinz–Kato inequality, have also been obtained. A nice application of the Heinz–Kato–Furuta inequality is given in [a1].
Additional references can be found in Heinz inequality.
References
| [a1] | M. Fujii, S. Izumino, R. Nakamoto, "Classes of operators determined by the Heinz–Kato–Furuta inequality and the Hölder–MacCarthy inequality" Nihonkai Math. J. , 5 (1994) pp. 61–67 |
| [a2] | T. Furuta, "An extension of the Heinz–Kato theorem" Proc. Amer. Math. Soc. , 120 (1994) pp. 785–787 |
Heinz-Kato-Furuta inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heinz-Kato-Furuta_inequality&oldid=16920