Erdös-Heilbronn problem
Let 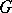 be an Abelian group and let
be an Abelian group and let 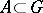 . For
. For 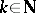 , let
, let
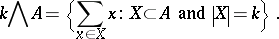 |
(Here, 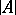 denotes the cardinality of a set
denotes the cardinality of a set 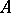 .) Let
.) Let 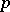 be a prime number and let
be a prime number and let 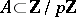 . It was conjectured by P. Erdös and H. Heilbronn that
. It was conjectured by P. Erdös and H. Heilbronn that 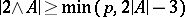 .
.
This conjecture, mentioned in [a5], was first proved in [a3], using linear algebra. As a consequence of the lower bound on the degree of the minimal polynomial of the Grasmann derivative, the following theorem is true [a3]: Let 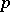 be a prime number and let
be a prime number and let 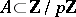 . Then
. Then
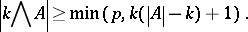 |
Applying this theorem with 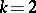 , one obtains the Erdös–Heilbronn conjecture mentioned above. A generalization of the theorem has been obtained in [a2]. Presently (1996), almost nothing is known for composite numbers. The following conjecture is proposed here: Let
, one obtains the Erdös–Heilbronn conjecture mentioned above. A generalization of the theorem has been obtained in [a2]. Presently (1996), almost nothing is known for composite numbers. The following conjecture is proposed here: Let  be a composite number (cf. also Prime number) and let
be a composite number (cf. also Prime number) and let 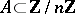 be such that
be such that 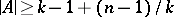 . Then
. Then  for some
for some 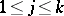 .
.
For a prime number  , the above conjecture is an easy consequence of the theorem above. Some applications to integer subset sums are contained in [a6]. Along the same lines, the conjecture has several implications. In particular, for
, the above conjecture is an easy consequence of the theorem above. Some applications to integer subset sums are contained in [a6]. Along the same lines, the conjecture has several implications. In particular, for 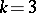 one finds: Let
one finds: Let 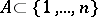 be such that
be such that 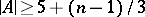 . Then there is a
. Then there is a 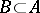 such that
such that 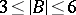 and
and 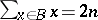 .
.
This was conjectured partially by Erdös and R. Graham [a5] and follows easily by applying the conjecture twice, after adding  .
.
References
| [a1] | N. Alon, "Subset sums" J. Number Th. , 27 (1987) pp. 196–205 |
| [a2] | N. Alon, M.B. Nathanson, I. Z. Rusza, "The polynomial method and restricted sums of congruence classes" J. Number Th. (to appear) |
| [a3] | J.A. Dias da Silva, Y.O. Hamidoune, "Cyclic subspaces of Grassmann derivations" Bull. London Math. Soc. , 26 (1994) pp. 140–146 |
| [a4] | P. Erdös, H. Heilbronn, "On the addition of residue classes mod 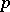 " Acta Arith. , 9 (1964) pp. 149–159 " Acta Arith. , 9 (1964) pp. 149–159 |
| [a5] | P. Erdös, R. Graham, "Old and new problems and results in combinatorial number theory" L'Enseign. Math. (1980) pp. 1–128 |
| [a6] | Y.O. Hamidoune, "The representation of some integers as a subset sum" Bull. London Math. Soc. , 26 (1994) pp. 557–563 |
| [a7] | H.B. Mann, "Addition theorems" , R.E. Krieger (1976) (Edition: Second) |
Erdös-Heilbronn problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Erd%C3%B6s-Heilbronn_problem&oldid=15547