Decidable set

A set of constructive objects (cf. Constructive object) of some fixed type which admits an algorithm for checking whether an element belongs to it. In fact one can restrict oneself to the concept of a decidable set of natural numbers, since the more general case can be reduced to this case by enumerating the objects under consideration. A set 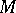of natural numbers is said to be decidable if there exists a general recursive function 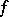such that 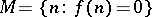. In this case 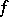is an algorithm for checking whether a natural number belongs to 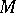. Actually, 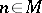is equivalent to 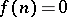. A decidable set of natural numbers is also often called a general recursive set or a recursive set.

In many well-known mathematical problems (such as the word identity problem, the homeomorphism problem, Hilbert's 10th problem, the "Entscheidungsproblem" in mathematical logic) one is required to prove or refute the assertion that a certain concrete set is decidable. Well-known (negative) solutions to the problems listed above consist of establishing that the sets corresponding to them are undecidable (see also Algorithmic problem).

References

[1]	E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964)

Comments

Decidable sets are also referred to as recursive or solvable. ([a3], p.11)

References

[a1]	H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) pp. 164–165
[a2]	S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) pp. 288