Absolute continuity

2020 Mathematics Subject Classification: Primary: 28A33 [MSN][ZBL]

Absolute continuity of the Lebesgue integral

Describes a property of absolutely Lebesgue integrable functions. Consider the Lebesgue measure $\mathcal{L}$ on the $n$-dimensional euclidean space and let $f\in L^1 (\mathbb R^n, \mathcal{L})$. Then for every $\varepsilon>0$ there is a $\delta>0$ such that \[ \left|\int_E f (x) d\mathcal{L} (x)\right| < \varepsilon \qquad \mbox{for every measurable set '"`UNIQ-MathJax7-QINU`"' with '"`UNIQ-MathJax8-QINU`"'}. \] This property can be generalized to measures $\mu$ on a $\sigma$-algebra $\mathcal{B}$ of subsets of a space $X$ and to functions $f\in L^1 (X, \mu)$.

Absolute continuity of measures

A concept in measure theory. If $\mu$ and $\nu$ are two measures on a $\sigma$-algebra $\mathcal{B}$ of subsets of $X$, we say that $\nu$ is absolutely continuous with respect to $\mu$ if $\nu (A) =0$ for any $A\in\mathcal{B}$ such that $\mu (A) =0$. This definition can be generalized to signed measures $\nu$ and even to vector-valued measure $\nu$. Some authors generalize it further to vector-valued $\mu$'s: in that case the absolute continuity of $\nu$ with respect to $\mu$ amounts to the requirement that $\nu (A) = 0$ for any $A\in\mathcal{B}$ such that $|\mu| (A)=0$, where $|\mu|$ is the total variation of $\mu$ (see Signed measure for the relevant definition).

The Radon-Nikodym theorem characterizes the absolute continuity of $\nu$ with respect to $\mu$ with the existence of a function $f\in L^1 (\mu)$ such that $\nu = f \mu$, i.e. such that \[ \nu (A) = \int_A f\, d\mu \qquad \mbox{for every '"`UNIQ-MathJax38-QINU`"'.} \] A corollary of the Radon-Nikodym, the Hahn decomposition theorem, characterize signed measures as differences of nonnegative measures. We refer to Radon-Nikodym for more on this topic.

Absolute continuity of a function is a stronger notion than continuity. A function 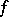defined on a segment 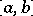is said to be absolutely continuous if for any 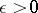there exists a 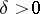such that for any finite system of pairwise non-intersecting intervals 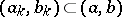, , 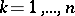for which

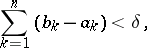the inequality

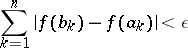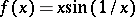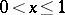holds. Any absolutely continuous function on a segment is continuous on this segment. The opposite implication is not true: e.g. the function if and 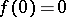is continuous on the segment 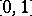, but is not absolutely continuous on it. If, in the definition of an absolutely continuous function, the requirement that the pairwise intersections of intervals 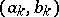are empty be discarded, then the function will satisfy an even stronger condition: A Lipschitz condition with some constant.

If two functions 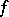and 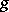are absolutely continuous, then their sum, difference and product are also absolutely continuous and, if does not vanish, so is their quotient 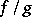. The superposition of two absolutely continuous functions need not be absolutely continuous. However, if the function 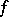is absolutely continuous on a segment 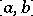and if 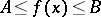, , 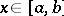while the function 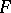satisfies a Lipschitz condition on the segment 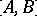, then the composite function 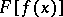is absolutely continuous on . 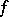If a function , which is absolutely continuous on 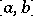, is monotone increasing, while 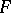is absolutely continuous on 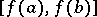, then the function 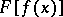is also absolutely continuous on .

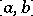An absolutely continuous function maps a set of measure zero into a set of measure zero, and a measurable set into a measurable set. Any continuous function of finite variation which maps each set of measure zero into a set of measure zero is absolutely continuous. Any absolutely continuous function can be represented as the difference of two absolutely continuous non-decreasing functions.

A function 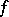that is absolutely continuous on the segment 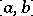has a finite variation on this segment and has a finite derivative 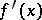at almost every point. The derivative 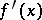is summable over this segment, and

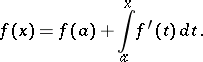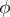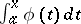If the derivative of an absolutely continuous function is almost everywhere equal to zero, then the function itself is constant. On the other hand, for any function that is summable on the function is absolutely continuous on this segment. Accordingly, the class of functions that are absolutely continuous on a given segment coincides with the class of functions that can be represented as an indefinite Lebesgue integral, i.e. as a Lebesgue integral with a variable upper limit of a certain summable function plus a constant.

If 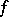is absolutely continuous on 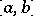, then its total variation is

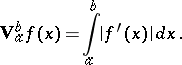The concept of absolute continuity can be generalized to include both functions of several variables and set functions (see Subsection 4 below).

References

[1]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[2]	V.I. Smirnov, "A course of higher mathematics" , 5 , Addison-Wesley (1964) (Translated from Russian)

L.D. Kudryavtsev

Absolute continuity of a set function is a concept usually applied to countably-additive functions defined on a 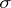-ring 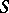of subsets of a set 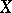. Thus, if 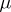and are two countably-additive functions defined on 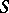having values in the extended real number line 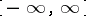, then is absolutely continuous with respect to 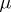(in symbols this is written as 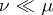) if 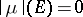entails . Here 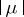is the total variation of :

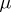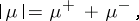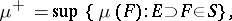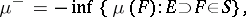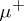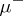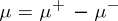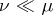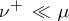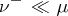and are measures, known as the positive and negative variations of ; according to the Jordan–Hahn theorem, . It turns out that the relations 1) ; 2) , ; 3) 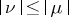are equivalent. If the measure is finite, 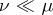if and only if for any 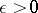there exists a 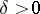such that 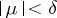entails 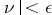. According to the Radon–Nikodým theorem, if 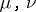are (completely) 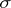-finite, (i.e. and there exists a sequence 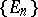, 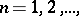such that

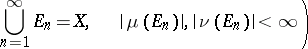and if 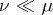, then there exists on 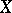a finite measurable function 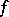such that

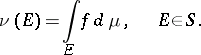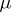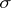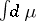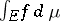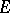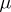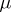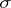Conversely, if is (completely) -finite and the integral makes sense, then as a function of the set is absolutely continuous with respect to . If and are (completely) -finite measures on 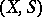, there exist uniquely defined (completely) 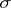-finite measures 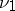and 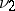such that 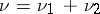, 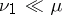and 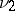is singular with respect to 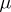(i.e. there exists a set 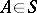such that 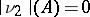, 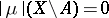) (Lebesgue's theorem). A measure, defined on the Borel sets of a finite-dimensional Euclidean space (or, more generally, of a locally compact group), is called absolutely continuous if it is absolutely continuous with respect to the Lebesgue (Haar) measure. A non-negative measure 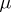on the Borel sets of the real line is absolutely continuous if and only if the corresponding distribution function 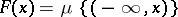is absolutely continuous (as a function of a real variable). The concept of absolute continuity of a set function can also be defined for finitely-additive functions and for functions with vector values.

References

[1]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)
[2]	J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970)

V.V. Sazonov

References

[a1]	H.L. Royden, "Real analysis" , Macmillan (1968)
[a2]	A.C. Zaanen, "Integration" , North-Holland (1967)
[a3]	W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953)
[a4]	W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 98
[a5]	A.E. Taylor, "General theory of functions and integration" , Blaisdell (1965)
[a6]	C.D. Aliprantz, O. Burleinshaw, "Principles of real analysis" , North-Holland (1981)