Skolem-Noether theorem
In its classical form, the Skolem–Noether theorem can be stated as follows. Let 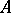 and
and 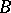 be finite-dimensional algebras over a field
be finite-dimensional algebras over a field 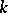 , and assume that
, and assume that 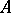 is simple and
is simple and 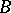 is central simple (cf. also Simple algebra; Central algebra; Field). If
is central simple (cf. also Simple algebra; Central algebra; Field). If 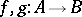 are
are 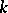 -algebra homomorphisms, then there exists an invertible
-algebra homomorphisms, then there exists an invertible 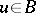 such that
such that
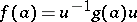 |
for all 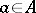 . A proof can be found, for example, in [a5], p. 21, or [a4], Chap, 4. In particular, every
. A proof can be found, for example, in [a5], p. 21, or [a4], Chap, 4. In particular, every 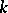 -algebra automorphism of a central simple algebra is inner (cf. also Inner automorphism). This can be generalized to an Azumaya algebra
-algebra automorphism of a central simple algebra is inner (cf. also Inner automorphism). This can be generalized to an Azumaya algebra 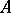 over a commutative ring
over a commutative ring 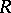 (cf. also Separable algebra): There is an exact sequence, usually called the Rosenberg–Zelinsky exact sequence:
(cf. also Separable algebra): There is an exact sequence, usually called the Rosenberg–Zelinsky exact sequence:
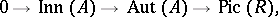 |
where 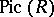 is the Picard group of
is the Picard group of 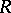 ,
,  is the group of
is the group of 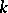 -algebra automorphisms of
-algebra automorphisms of 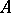 and
and 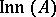 is the subgroup consisting of inner automorphisms. The proof is an immediate application of the categorical characterization of Azumaya algebras: An
is the subgroup consisting of inner automorphisms. The proof is an immediate application of the categorical characterization of Azumaya algebras: An 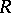 -algebra
-algebra 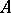 is Azumaya if and only if the categories of
is Azumaya if and only if the categories of  -modules and
-modules and 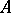 -bimodules are equivalent via the functors sending an
-bimodules are equivalent via the functors sending an 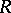 -module
-module 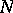 to
to 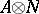 , and sending an
, and sending an 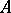 -bimodule
-bimodule 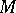 to
to
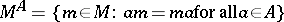 |
(see, e.g., [a6], IV.1, for details).
The Skolem–Noether theorem plays a crucial role in the theory of the Brauer group; for example, it is used in the proof of the Hilbert 90 theorem (cf. also Hilbert theorem) and the cross product theorem. There exist versions of the Skolem–Noether theorem (and the Rosenberg–Zelinsky exact sequence) for other generalized types of Azumaya algebras; in particular, for Azumaya algebras over schemes [a3], Azumaya algebras relative to a torsion theory [a7], III.3.26, and Long's 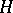 -dimodule Azumaya algebras [a1], [a2].
-dimodule Azumaya algebras [a1], [a2].
References
| [a1] | M. Beattie, "Automorphisms of 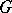 -Azumaya algebras" Canad. J. Math. , 37 (1985) pp. 1047–1058 -Azumaya algebras" Canad. J. Math. , 37 (1985) pp. 1047–1058 |
| [a2] | S. Caenepeel, "Brauer groups, Hopf algebras and Galois theory" , K-Monographs Math. , 4 , Kluwer Acad. Publ. (1998) |
| [a3] | A. Grothendieck, "Le groupe de Brauer I" , Dix Exposés sur la cohomologie des schémas , North-Holland (1968) |
| [a4] | I.N. Herstein, "Noncommutative rings" , Carus Math. Monographs , 15 , Math. Assoc. Amer. (1968) |
| [a5] | I. Kersten, "Brauergruppen von Körpern" , Aspekte der Math. , D6 , Vieweg (1990) |
| [a6] | M.A. Knus, M. Ojanguren, "Théorie de la descente et algèbres d'Azumaya" , Lecture Notes in Mathematics , 389 , Springer (1974) |
| [a7] | F. Van Oystaeyen, A. Verschoren, "Relative invariants of rings I" , Monographs and Textbooks in Pure and Appl. Math. , 79 , M. Dekker (1983) |
Skolem-Noether theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Skolem-Noether_theorem&oldid=15101