Weierstrass coordinates
A type of coordinates in an elliptic space. Let $M^n$ be an elliptic space obtained by the identification of diametrically-opposite points of the unit sphere $S^n$ in $(n+1)$-dimensional Euclidean space. The Weierstrass coordinates $(x_0 ,\ldots, x_n)$ of a point in $M^n$ are the orthogonal Cartesian coordinates of the point of $S^n$ that corresponds to it. Since the isometric mapping of $M^n$ into $S^n$ is not single-valued, Weierstrass coordinates are defined up to sign. A hyperplane in $M^n$ is given by a homogeneous linear equation
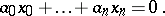 |
Named after K. Weierstrass, who used these coordinates in his courses on Lobachevskii geometry in 1872.
Comments
These coordinates for elliptic space can be normalized so that
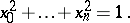 |
The analogous Weierstrass coordinates for hyperbolic space satisfy
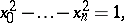 |
with the same equation  for a hyperplane.
for a hyperplane.
References
| [a1] | H. Liebmann, "Nichteuklidische Geometrie" , Göschen (1912) pp. 114–119 |
| [a2] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 121, 281 |
Weierstrass coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_coordinates&oldid=15072