Cayley-Darboux equation
From Encyclopedia of Mathematics
Revision as of 18:51, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Cayley–Darboux equation to Cayley-Darboux equation: ascii title)
A third-order partial differential equation that must be necessarily satisfied by a function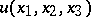 
in order for the family of surfaces 
to be complementable to a triply orthogonal system of surfaces. The Cayley–Darboux equation may be written as
 |
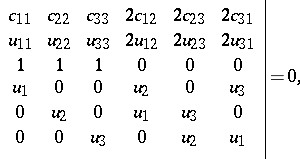where
 |
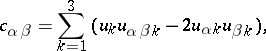and
 |
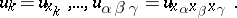The equation was first obtained in explicit form by A. Cayley [1]. The above form of the equation is due to G. Darboux [2].
References
| [1] | A. Cayley, "Sur la condition pour qu'une famille de surfaces données puisse faire partie d'un système orthogonal" C.R. Acad. Sci. Paris , 75 (1872) pp. 324–330; 381–385 (Also: Collected mathematical papers, Vol. 8 (1891), pp. 269–291) |
| [2] | G. Darboux, "Leçons sur les systèmes orthogonaux et les coordonnées curvilignes" , Paris (1898) |
| [3] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 2 , Moscow-Leningrad (1948) (In Russian) |
How to Cite This Entry:
Cayley-Darboux equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cayley-Darboux_equation&oldid=14903
Cayley-Darboux equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cayley-Darboux_equation&oldid=14903
This article was adapted from an original article by E.V. Shikin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article