Symplectic structure
An infinitesimal structure of order one on an even-dimensional smooth orientable manifold  which is defined by a non-degenerate
which is defined by a non-degenerate  -form
-form  on
on  . Every tangent space
. Every tangent space  has the structure of a symplectic space with skew-symmetric scalar product
has the structure of a symplectic space with skew-symmetric scalar product  . All frames tangent to
. All frames tangent to  adapted to the symplectic structure (that is, frames with respect to which
adapted to the symplectic structure (that is, frames with respect to which  has the canonical form
has the canonical form  ) form a principal fibre bundle over
) form a principal fibre bundle over 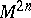 whose structure group is the symplectic group
whose structure group is the symplectic group 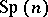 . Specifying a symplectic structure on
. Specifying a symplectic structure on  is equivalent to specifying an
is equivalent to specifying an 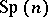 -structure on
-structure on  (cf.
(cf. 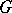 -structure).
-structure).
Given a symplectic structure on 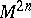 , there is an isomorphism between the modules of vector fields and
, there is an isomorphism between the modules of vector fields and  -forms on
-forms on 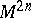 , under which a vector field
, under which a vector field 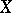 is associated with a
is associated with a 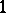 -form,
-form, 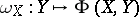 . In this context, the image of the Lie bracket
. In this context, the image of the Lie bracket 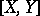 is called the Poisson bracket
is called the Poisson bracket 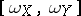 . In particular, when
. In particular, when 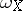 and
and 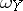 are exact differentials, one obtains the concept of the Poisson bracket of two functions on
are exact differentials, one obtains the concept of the Poisson bracket of two functions on 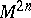 , which generalizes the corresponding classical concept.
, which generalizes the corresponding classical concept.
A symplectic structure is also called an almost-Hamiltonian structure, and if 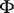 is closed, i.e.
is closed, i.e. 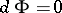 , a Hamiltonian structure, though the condition
, a Hamiltonian structure, though the condition 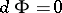 is sometimes included in the definition of a symplectic structure. These structures find application in global analytical mechanics, since the cotangent bundle
is sometimes included in the definition of a symplectic structure. These structures find application in global analytical mechanics, since the cotangent bundle  of any smooth manifold
of any smooth manifold 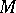 admits a canonical Hamiltonian structure. It is defined by the form
admits a canonical Hamiltonian structure. It is defined by the form 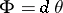 , where the
, where the  -form
-form 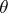 on
on 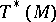 , called the Liouville form, is given by:
, called the Liouville form, is given by: 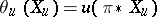 for any tangent vector
for any tangent vector 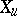 at the point
at the point 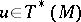 , where
, where 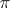 is the projection
is the projection 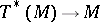 . If one chooses local coordinates
. If one chooses local coordinates  on
on 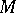 , and
, and 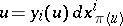 , then
, then  , so that
, so that 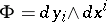 . In classical mechanics
. In classical mechanics 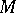 is interpreted as the configuration space and
is interpreted as the configuration space and 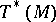 as the phase space.
as the phase space.
A vector field 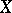 on a manifold
on a manifold 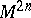 with a Hamiltonian structure is called a Hamiltonian vector field (or a Hamiltonian system) if the
with a Hamiltonian structure is called a Hamiltonian vector field (or a Hamiltonian system) if the 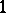 -form
-form 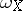 is closed. If, in addition, it is exact, that is,
is closed. If, in addition, it is exact, that is, 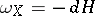 , then
, then 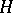 is called a Hamiltonian on
is called a Hamiltonian on  and is a generalization of the corresponding classical concept.
and is a generalization of the corresponding classical concept.
References
| [1] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [2] | C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) |
Comments
Mostly, for a symplectic structure on a manifold the defining  -form
-form 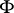 is required to be closed (cf. [a1], p. 176, [a4], p. 36ff). If
is required to be closed (cf. [a1], p. 176, [a4], p. 36ff). If 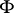 is not necessarily closed, one speaks of an almost-symplectic structure.
is not necessarily closed, one speaks of an almost-symplectic structure.
Let  denote the vector field on a symplectic manifold
denote the vector field on a symplectic manifold  that corresponds to the
that corresponds to the 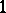 -form
-form  . Then the Poisson bracket on
. Then the Poisson bracket on 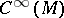 is defined by
is defined by
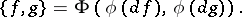 |
This turns 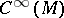 into a Lie algebra which satisfies the Leibniz property
into a Lie algebra which satisfies the Leibniz property
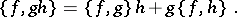 | (*) |
More generally, an algebra  which has an extra Lie bracket
which has an extra Lie bracket 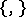 so that (*) is satisfied is called a Poisson algebra. A smooth manifold
so that (*) is satisfied is called a Poisson algebra. A smooth manifold 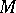 with a Poisson algebra structure on
with a Poisson algebra structure on 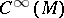 is called a Poisson manifold, [a4], p. 107ff.
is called a Poisson manifold, [a4], p. 107ff.
References
| [a1] | R. Abraham, J.E. Marsden, "Foundations of mechanics" , Benjamin/Cummings (1978) |
| [a2] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
| [a3] | J.M. Souriau, "Structures des systèmes dynamiques" , Dunod (1969) |
| [a4] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) (Translated from French) |
| [a5] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [a6] | V.I. [V.I. Arnol'd] Arnold, A.B. [A.B. Givent'al] Giventhal, "Symplectic geometry" , Dynamical Systems , IV , Springer (1990) (Translated from Russian) |
| [a7] | A. Crumeyrolle (ed.) J Grifone (ed.) , Symplectic geometry , Pitman (1983) |
Symplectic structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symplectic_structure&oldid=14696