Bivector space
A centro-affine space  (where
(where 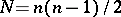 ), which may be assigned to each point of a space
), which may be assigned to each point of a space 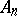 with an affine connection (in particular, to a Riemannian space
with an affine connection (in particular, to a Riemannian space 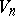 ). Consider all tensors with even covariant and contravariant valencies at a point of the space
). Consider all tensors with even covariant and contravariant valencies at a point of the space 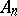 (or
(or 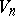 ); the covariant and contravariant indices are subdivided into different pairs, for each one of which the tensor is skew-symmetric. Tensors with these two properties are called bitensors. If each skew-symmetric pair is regarded as a collective index, the number of new indices will be
); the covariant and contravariant indices are subdivided into different pairs, for each one of which the tensor is skew-symmetric. Tensors with these two properties are called bitensors. If each skew-symmetric pair is regarded as a collective index, the number of new indices will be 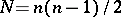 . The simplest bitensor is the bivector
. The simplest bitensor is the bivector
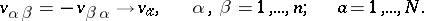 |
If, at a point  of
of 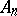 ,
,
 |
 |
then 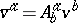 , and the set of bivectors assigned to
, and the set of bivectors assigned to 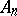 (or
(or 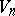 ) at a given point defines a vector space of dimension
) at a given point defines a vector space of dimension 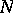 such that the components satisfy the conditions
such that the components satisfy the conditions
 |
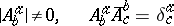 |
i.e. this set defines the centro-affine space 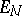 , called the bivector space at the given point. In
, called the bivector space at the given point. In 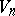 the bivector space may be metrized with the aid of the metric tensor
the bivector space may be metrized with the aid of the metric tensor
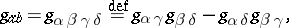 |
after which 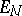 becomes a metric space
becomes a metric space 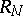 .
.
Bivector spaces are used in Riemannian geometry and in the general theory of relativity. The bivector space 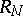 is constructed at a given point of the space
is constructed at a given point of the space 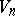 , and different representations of the curvature tensor with components
, and different representations of the curvature tensor with components 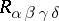 ,
, 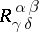 ,
, 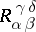 and the second-valency bitensors with components
and the second-valency bitensors with components 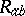 ,
, 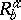 ,
, 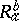 are associated, respectively. The study of the algebraic structure of the curvature tensor may then be reduced to the study of the pencil of quadratic forms
are associated, respectively. The study of the algebraic structure of the curvature tensor may then be reduced to the study of the pencil of quadratic forms 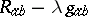 , the second one of which is non-degenerate (
, the second one of which is non-degenerate (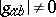 ). The study of elementary divisors of this pair results in a classification of the spaces
). The study of elementary divisors of this pair results in a classification of the spaces 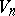 . If
. If  (
(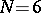 ) and if the form
) and if the form 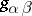 has signature
has signature  , then it can be shown that only three types of Einstein spaces exist.
, then it can be shown that only three types of Einstein spaces exist.
A bivector may be assigned to each rotation in 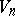 ; this means that in
; this means that in  there corresponds a vector, which is convenient for the study of infinitesimal transformations. Essentially, a bivector space is identical with a biplanar space [2].
there corresponds a vector, which is convenient for the study of infinitesimal transformations. Essentially, a bivector space is identical with a biplanar space [2].
References
| [1] | A.Z. Petrov, "New methods in general relativity theory" , Moscow (1966) (In Russian) |
| [2] | A.P. Norden, "On complex representation of tensors of a biplanar space" , 8 Kazan. Gos. Univ. Uchen. Zap. , 114 (1954) pp. 45–53 (In Russian) MR76400 |
Comments
Consider a bivector as represented by an ordered pair of vectors 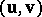 as in [a1], [a4] or the article bivector. The Plücker coordinates of
as in [a1], [a4] or the article bivector. The Plücker coordinates of 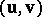 ,
, 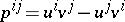 , then constitute a bivector as in the article above. Let
, then constitute a bivector as in the article above. Let 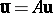 ,
, 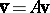 , i.e.
, i.e. 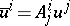 and similarly for
and similarly for  . Then the
. Then the 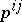 transform as
transform as 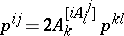 . Whence the formulas above. Here the square brackets in
. Whence the formulas above. Here the square brackets in 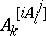 are a notation signifying taking an alternating average. Thus
are a notation signifying taking an alternating average. Thus 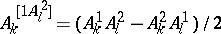 . If certain indices are to be singled out, i.e. exempt from this averaging process, this is indicated by
. If certain indices are to be singled out, i.e. exempt from this averaging process, this is indicated by  . Thus
. Thus 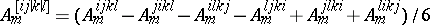 , and
, and 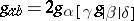 , cf. above. This is a notation introduced by R. Bach [a5]. Cf. also Alternation.
, cf. above. This is a notation introduced by R. Bach [a5]. Cf. also Alternation.
In more modern terms what is described here is the bundle of bivectors over  .
.
A centro-affine space is an affine space with a distinguished point, i.e. practically a vector space. It is not a term which is still greatly used.
References
| [a1] | E. Cartan, "Geometry of Riemannian spaces. (With notes and appendices by R. Hermann)" , Math. Sci. Press (1963) (Translated from French) |
| [a2] | S. Gołab, "Tensor calculus" , Elsevier (1974) (Translated from Polish) Zbl 0277.53008 |
| [a3] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [a4] | J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) pp. 11ff (Translated from German) MR0066025 Zbl 0057.37803 |
| [a5] | R. Bach, "Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungsbegriffs" Math. Zeitschr. , 9 (1921) pp. 110–135 MR1544454 |
Bivector space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bivector_space&oldid=14487