Bivector space

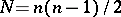A centro-affine space (where ), which may be assigned to each point of a space 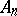with an affine connection (in particular, to a Riemannian space 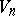). Consider all tensors with even covariant and contravariant valencies at a point of the space 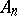(or 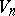); the covariant and contravariant indices are subdivided into different pairs, for each one of which the tensor is skew-symmetric. Tensors with these two properties are called bitensors. If each skew-symmetric pair is regarded as a collective index, the number of new indices will be 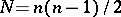. The simplest bitensor is the bivector

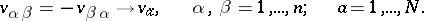If, at a point 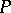of ,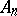

then 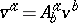, and the set of bivectors assigned to 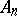(or 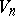) at a given point defines a vector space of dimension 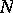such that the components satisfy the conditions

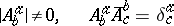i.e. this set defines the centro-affine space 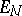, called the bivector space at the given point. In 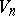the bivector space may be metrized with the aid of the metric tensor

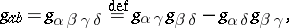after which 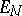becomes a metric space .

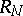Bivector spaces are used in Riemannian geometry and in the general theory of relativity. The bivector space 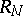is constructed at a given point of the space 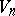, and different representations of the curvature tensor with components 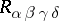, , 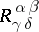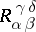and the second-valency bitensors with components 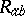, , 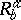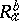are associated, respectively. The study of the algebraic structure of the curvature tensor may then be reduced to the study of the pencil of quadratic forms 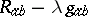, the second one of which is non-degenerate (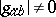). The study of elementary divisors of this pair results in a classification of the spaces 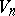. If (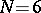) and if the form 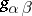has signature , then it can be shown that only three types of Einstein spaces exist.

A bivector may be assigned to each rotation in 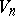; this means that in there corresponds a vector, which is convenient for the study of infinitesimal transformations. Essentially, a bivector space is identical with a biplanar space [2].

References

[1]	A.Z. Petrov, "New methods in general relativity theory" , Moscow (1966) (In Russian)
[2]	A.P. Norden, "On complex representation of tensors of a biplanar space" , 8 Kazan. Gos. Univ. Uchen. Zap. , 114 (1954) pp. 45–53 (In Russian)

Comments

Consider a bivector as represented by an ordered pair of vectors 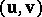as in [a1], [a4] or the article bivector. The Plücker coordinates of 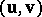, , 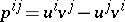then constitute a bivector as in the article above. Let 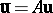, , 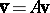i.e. 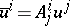and similarly for . Then the 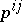transform as 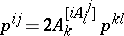. Whence the formulas above. Here the square brackets in 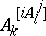are a notation signifying taking an alternating average. Thus 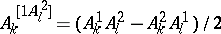. If certain indices are to be singled out, i.e. exempt from this averaging process, this is indicated by . 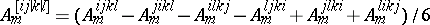Thus , and 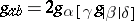, cf. above. This is a notation introduced by R. Bach [a5]. Cf. also Alternation.

In more modern terms what is described here is the bundle of bivectors over .

A centro-affine space is an affine space with a distinguished point, i.e. practically a vector space. It is not a term which is still greatly used.

References

[a1]	E. Cartan, "Geometry of Riemannian spaces. (With notes and appendices by R. Hermann)" , Math. Sci. Press (1963) (Translated from French)
[a2]	S. Gołab, "Tensor calculus" , Elsevier (1974) (Translated from Polish)
[a3]	P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)
[a4]	J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) pp. 11ff (Translated from German)
[a5]	R. Bach, "Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungsbegriffs" Math. Zeitschr. , 9 (1921) pp. 110–135