Triangular norm

t-norm

A binary operation on the unit interval 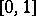, i.e., a function 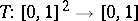such that for all 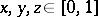the following four axioms are satisfied:

T1) (commutativity) ;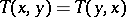

T2) (associativity) ;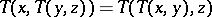

T3) (monotonicity) 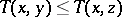whenever ;

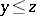T4) (boundary condition) .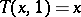

If 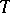is a triangular norm, then its dual triangular co-norm 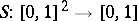is given by

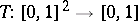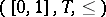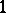A function is a triangular norm if and only if is a fully ordered commutative semi-group (cf. [a3] and -group) with neutral element and annihilator , where 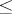is the usual order on .

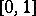For each -semi-group , i.e. a semi-group in which the binary associative operation on the closed subinterval 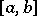of the extended real line is continuous and one of the boundary points of 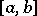acts as a neutral element and the other one as an annihilator ([a6], [a7]), there exists a continuous triangular norm or a continuous triangular co-norm 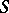such that the linear transformation 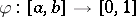given by

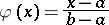is an isomorphism between 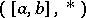and eithe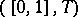r or .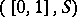

The following are the four basic triangular norms, together with their dual triangular co-norms:

i) the minimum 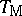and maximum 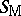, given by

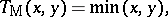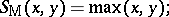ii) the product 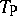and probabilistic sum 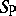, given by

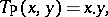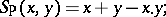iii) the Lukasiewicz triangular norm 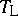and Lukasiewicz triangular co-norm 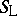, given by

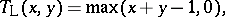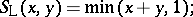iv) the weakest triangular norm (or drastic product) 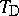and strongest triangular co-norm 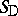, given by

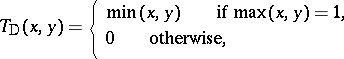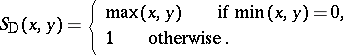Let be a family of triangular norms and let 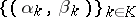be a family of pairwise disjoint open subintervals of the unit interval 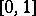(i.e., is an at most countable index set). Consider the linear transformations 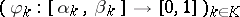given by

Then the function 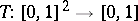defined by

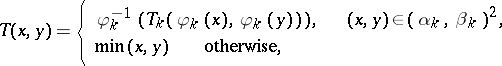is a triangular norm, which is called the ordinal sum of the summands , .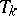

The following representations hold ([a1], [a5], [a6]):

A function 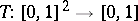is a continuous Archimedean triangular norm, i.e., for all 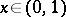one has 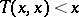, if and only if there exists a continuous, strictly decreasing function 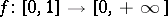with 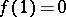such that for all ,

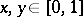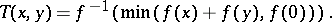The function 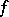is then called an additive generator of 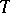; it is uniquely determined by up to a positive multiplicative constant.

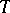is a continuous triangular norm if and only if 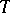is an ordinal sum whose summands are continuous Archimedean triangular norms.

Triangular norms are applied in many fields, such as probabilistic metric spaces [a9], [a4], fuzzy sets, fuzzy logics and their applications [a4], the theory of generalized measures [a2], [a8], functional equations [a1] and in non-linear differential and difference equations (see [a4], [a8]).

References

[a1]	J. Aczél, "Lectures on functional equations and their applications" , Acad. Press (1969)
[a2]	D. Butnariu, E.P. Klement, "Triangular norm-based measures and games with fuzzy coalitions" , Kluwer Acad. Publ. (1993)
[a3]	L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) Zbl 0137.02001
[a4]	E.P. Klement, R. Mesiar, E. Pap, "Triangular norms" Trends in Logic--Studia Logica Library 8 Kluwer Academic ISBN 0-7923-6416-3 Zbl 0972.03002
[a5]	C.M. Ling, "Representation of associative functions" Publ. Math. Debrecen , 12 (1965) pp. 189–212
[a6]	P.S. Mostert, A.L. Shields, "On the structure of semigroups on a compact manifold with boundary" Ann. of Math. , 65 (1957) pp. 117–143
[a7]	A.B. Paalman-de Miranda, "Topological semigroups" , Tracts , 11 , Math. Centre Amsterdam (1970)
[a8]	E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995)
[a9]	B. Schweizer, A. Sklar, "Probabilistic metric spaces" , North-Holland (1983)