Gauss kernel
From Encyclopedia of Mathematics
Revision as of 09:09, 4 May 2012 by Boris Tsirelson (talk | contribs) (→References: Feller: internal link)
The  -dimensional Gauss (or Weierstrass) kernel
-dimensional Gauss (or Weierstrass) kernel
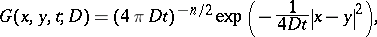 |
with 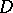 a positive constant,
a positive constant, 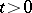 ,
, 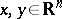 , is the fundamental solution of the
, is the fundamental solution of the  -dimensional heat equation
-dimensional heat equation 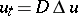 . Moreover, this kernel is an approximate identity in that the Gauss–Weierstrass singular integral at the function
. Moreover, this kernel is an approximate identity in that the Gauss–Weierstrass singular integral at the function 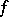 ,
,
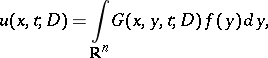 |
satisfies 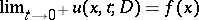 almost everywhere, for example, whenever
almost everywhere, for example, whenever 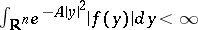 for some
for some 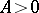 ; see [a4]. Thus
; see [a4]. Thus 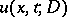 is a solution of the heat equation for
is a solution of the heat equation for 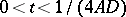 ,
,  having the initial "temperature"
having the initial "temperature" 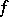 .
.
In the theory of Markov processes (cf. Markov process) the Gauss kernel gives the transition probability density of the Wiener–Lévy process (or of Brownian motion). The semi-group property of the Gauss kernel
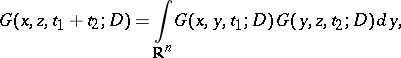 |
 |
is essential here.
References
| [a1] | P. Butzer, R. Nessel, "Fourier analysis and approximation", I, Birkhäuser (1971) |
| [a2] | R. Courant, D. Hilbert, "Methods of mathematical physics", II, Wiley (1962) |
| [a3] | W. Feller, "An introduction to probability theory and its applications", 2, Springer (1976) (Edition: Second) |
| [a4] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals", Clarendon Press (1937) |
| [a5] | K. Weierstrass, "Ueber die analytische Darstellbarkeit sogenannter willkurlichen Functionen reeler Argumente" Berliner Sitzungsberichte (1985) pp. 633–639; 789–805 |
How to Cite This Entry:
Gauss kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_kernel&oldid=13441
Gauss kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss_kernel&oldid=13441
This article was adapted from an original article by R. Kerman (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article