Inertial prime number
inert prime number, in an extension 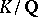
A prime number 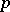 such that the principal ideal generated by
such that the principal ideal generated by  remains prime in
remains prime in 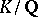 , where
, where 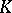 is a finite extension of the field of rational numbers
is a finite extension of the field of rational numbers 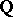 ; in other words, the ideal
; in other words, the ideal 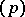 is prime in
is prime in 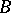 , where
, where 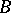 is the ring of integers of
is the ring of integers of  . In this case one also says that
. In this case one also says that 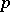 is inert in the extension
is inert in the extension 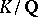 . By analogy, a prime ideal
. By analogy, a prime ideal 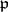 of a Dedekind ring
of a Dedekind ring 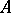 is said to be inert in the extension
is said to be inert in the extension 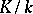 , where
, where  is the field of fractions of
is the field of fractions of 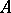 and
and 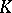 is a finite extension of
is a finite extension of 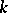 , if the ideal
, if the ideal 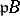 , where
, where 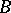 is the integral closure of
is the integral closure of 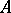 in
in 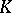 , is prime.
, is prime.
If 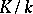 is a Galois extension with Galois group
is a Galois extension with Galois group 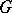 , then for any ideal
, then for any ideal 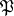 of the ring
of the ring 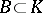 , a subgroup
, a subgroup 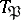 of the decomposition group
of the decomposition group 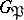 of the ideal
of the ideal 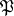 is defined which is called the inertia group (see Ramified prime ideal). The extension
is defined which is called the inertia group (see Ramified prime ideal). The extension  is a maximal intermediate extension in
is a maximal intermediate extension in 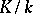 in which the ideal
in which the ideal 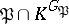 is inert.
is inert.
In cyclic extensions of algebraic number fields there always exist infinitely many inert prime ideals.
References
| [1] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) |
| [2] | H. Weyl, "Algebraic theory of numbers" , Princeton Univ. Press (1959) |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Comments
Let 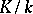 be a Galois extension with Galois group
be a Galois extension with Galois group  . Let
. Let 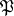 be a prime ideal of (the ring of integers
be a prime ideal of (the ring of integers 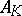 ) of
) of 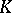 . The decomposition group of
. The decomposition group of  is defined by
is defined by  . The subgroup
. The subgroup 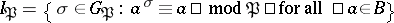 is the inertia group of
is the inertia group of 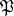 over
over 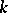 . It is a normal subgroup of
. It is a normal subgroup of 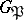 . The subfields of
. The subfields of 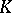 which, according to Galois theory, correspond to
which, according to Galois theory, correspond to 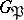 and
and 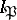 , are called respectively the decomposition field and inertia field of
, are called respectively the decomposition field and inertia field of 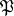 .
.
Inertial prime number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inertial_prime_number&oldid=13151