Brown-Peterson spectrum
By the Pontryagin–Thom theorem, there is a ring spectrum 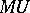 (cf. Spectrum of a ring) whose homotopy is isomorphic to the graded ring of bordism classes of closed smooth manifolds with a complex structure on their stable normal bundles (cf. also Cobordism). E.H. Brown and F.P. Peterson [a1] showed that, when localized at a prime
(cf. Spectrum of a ring) whose homotopy is isomorphic to the graded ring of bordism classes of closed smooth manifolds with a complex structure on their stable normal bundles (cf. also Cobordism). E.H. Brown and F.P. Peterson [a1] showed that, when localized at a prime  , the spectrum
, the spectrum 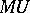 is homotopy equivalent to the wedge of various suspensions (cf. also Suspension) of a ring spectrum
is homotopy equivalent to the wedge of various suspensions (cf. also Suspension) of a ring spectrum 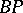 , the Brown–Peterson spectrum. The homotopy of this spectrum is the polynomial algebra
, the Brown–Peterson spectrum. The homotopy of this spectrum is the polynomial algebra
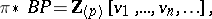 |
where the degree of 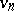 is
is 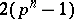 . As a module over the Steenrod algebra,
. As a module over the Steenrod algebra,
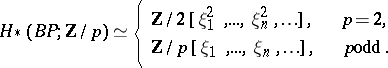 |
Four properties of 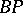 have made it one of the most useful spectra in homotopy theory. First, D. Quillen [a5] determined the structure of its ring of operations. Second, A. Liulevicius [a3] and M. Hazewinkel [a2] constructed polynomial generators of
have made it one of the most useful spectra in homotopy theory. First, D. Quillen [a5] determined the structure of its ring of operations. Second, A. Liulevicius [a3] and M. Hazewinkel [a2] constructed polynomial generators of 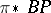 with good properties. Third, the Baas–Sullivan construction can be used to construct simple spectra from
with good properties. Third, the Baas–Sullivan construction can be used to construct simple spectra from 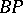 with very nice properties. The most notable of these spectra are the Morava
with very nice properties. The most notable of these spectra are the Morava 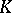 -theories
-theories 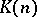 , which are central in the statement of the periodicity theorem. (See [a7] for an account of the nilpotence and periodicity theorems.) Fourth, S.P. Novikov [a4] constructed the Adams–Novikov spectral sequence, which uses knowledge of the Brown–Peterson homology of a spectrum
, which are central in the statement of the periodicity theorem. (See [a7] for an account of the nilpotence and periodicity theorems.) Fourth, S.P. Novikov [a4] constructed the Adams–Novikov spectral sequence, which uses knowledge of the Brown–Peterson homology of a spectrum  to compute the homotopy of
to compute the homotopy of  . (See [a6] for a survey of how the Adams–Novikov spectral sequence gives information on the stable homotopy groups of spheres.)
. (See [a6] for a survey of how the Adams–Novikov spectral sequence gives information on the stable homotopy groups of spheres.)
An introduction to the study of 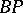 is given in [a8].
is given in [a8].
References
| [a1] | E.H. Brown, F.P. Peterson, "A spectrum whose 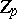 -homology is the algebra of reduced -homology is the algebra of reduced 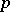 th powers" Topology , 5 (1966) pp. 149–154 th powers" Topology , 5 (1966) pp. 149–154 |
| [a2] | M. Hazewinkel, "Constructing formal groups III. Applications to complex cobordism and Brown–Peterson cohomology" J. Pure Appl. Algebra , 10 (1977/78) pp. 1–18 |
| [a3] | A. Liulevicius, "On the algebra 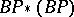 " , Lecture Notes in Mathematics , 249 , Springer (1971) pp. 47–53 " , Lecture Notes in Mathematics , 249 , Springer (1971) pp. 47–53 |
| [a4] | S.P. Novikov, "The methods of algebraic topology from the viewpoint of cobordism theories" Math. USSR Izv. (1967) pp. 827–913 Izv. Akad. Nauk SSSR Ser. Mat. , 31 (1967) pp. 855–951 |
| [a5] | D. Quillen, "On the formal group laws of unoriented and complex cobordism theory" Bull. Amer. Math. Soc. , 75 (1969) pp. 1293–1298 |
| [a6] | D.C. Ravenel, "Complex cobordism and stable homotopy groups of spheres" , Pure and Applied Mathematics , 121 , Acad. Press (1986) |
| [a7] | D.C. Ravenel, "Nilpotence and periodicity in stable homotopy theory" , Annals of Math. Stud. , 128 , Princeton Univ. Press (1992) |
| [a8] | W.S. Wilson, "Brown–Peterson homology, an introduction and sampler" , Regional Conf. Ser. Math. , 48 , Amer. Math. Soc. (1982) |
Brown-Peterson spectrum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brown-Peterson_spectrum&oldid=13107