Integration by parts
One of the methods for calculating integrals. It consists in representing an integral of an expression of the form 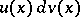 by an integral of
by an integral of 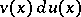 . For a definite integral the formula of integration by parts is
. For a definite integral the formula of integration by parts is
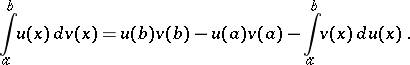 | (1) |
It is applicable under the assumptions that  ,
,  and their derivatives
and their derivatives 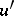 ,
, 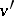 are continuous on
are continuous on 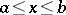 .
.
The analogue of (1) for an indefinite integral is
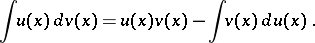 | (2) |
The analogue of (1) for a multiple integral is
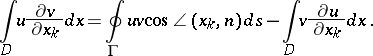 | (3) |
Here 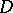 is a domain in
is a domain in 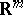 with smooth (or at least piecewise-smooth) boundary
with smooth (or at least piecewise-smooth) boundary 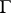 ;
; 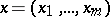 ; and
; and 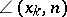 is the angle between the
is the angle between the 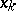 -axis and the outward normal to
-axis and the outward normal to  . Formula (3) holds if, e.g.,
. Formula (3) holds if, e.g.,  ,
,  and their first-order partial derivatives are continuous on
and their first-order partial derivatives are continuous on 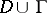 . If the integrals in (3) are understood as Lebesgue integrals, then the formula is true if
. If the integrals in (3) are understood as Lebesgue integrals, then the formula is true if  and
and  belong to a Sobolev space:
belong to a Sobolev space:  ,
, 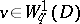 for any
for any  with
with 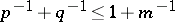 .
.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , 1–2 , Moscow (1970) (In Russian) MR1617334 MR1070567 MR1070566 MR1070565 MR0866891 MR0767983 MR0767982 MR0628614 MR0619214 Zbl 1080.00002 Zbl 1080.00001 Zbl 1060.26002 Zbl 0869.00003 Zbl 0696.26002 Zbl 0703.26001 Zbl 0609.00001 Zbl 0632.26001 Zbl 0485.26002 Zbl 0485.26001 |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) Zbl 0397.00003 Zbl 0384.00004 |
Comments
Formula (1) is valid whenever both  and
and  are absolutely continuous (cf. Absolute continuity, 3)) on the closed interval
are absolutely continuous (cf. Absolute continuity, 3)) on the closed interval  . In this generality the integral must be taken in the Lebesgue sense (cf. Lebesgue integral).
. In this generality the integral must be taken in the Lebesgue sense (cf. Lebesgue integral).
For additional references see also Improper integral.
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202 |
| [a2] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) MR0604364 Zbl 0454.26001 |
Integration by parts. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integration_by_parts&oldid=13008